1. Общие сведения о задаче сжатия данных
Задачей сжатия данных является минимизация технических затрат на
хранение или передачу данных путем оптимального кодирования источников [1, стр. 75].
Согласно классической схеме системы связи [1, 2], сжатие данных, т.е. более компактное их
представление производится в кодере источника, а задачей декодера источника является
соответственно восстановление сжатых данных.
Используя материалы [1-3], укажем основные понятия,
связанные с задачей сжатия данных.
Несущественная информация
- это информация, которой можно пренебречь при передаче. Например, телефонная связь использует полосу
частот в диапазоне 3,4 кГц. Все остальные спектральные составляющие речи отбрасываются, при этом
существенная часть информации теряется. Ясно, что первоначальный сигнал не может быть восстановлен
полностью. В этом случае говорят о кодировании с потерями.
Избыточная информация - неоднократное повторение в сообщении необходимой для приемника информации.
Избыточность может быть устранена без потери информации. Если алгоритм кодирования отбрасывает только избыточную
информацию, то говорят о кодировании без потерь.
Степень сжатия 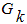 определяется затратами для передачи или хранения информации без сжатия
определяется затратами для передачи или хранения информации без сжатия 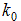 и затратами с использованием некоторого метода сжатия
и затратами с использованием некоторого метода сжатия 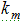
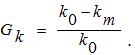
Средняя длина кода вычисляется как сумма длин двоичных кодов, взвешенных вероятностью этих кодовых символов:
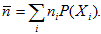
Коды сжатия можно классифицировать как коды
фиксированной и переменной длины, префиксные и непрефиксные коды.
Перечислим, согласно [2], желаемые свойства полезных кодов источника.
1. Свойство единственности декодирования. Единственным образом
декодируемые коды позволяют однозначно отображать сжатые данные в исходные.
2. Свойство мгновенной декодируемости. Мгновенно декодируемый
код – это такой код, для которого граница настоящего кодового слова
может быть определена концом настоящего кодового слова, а не началом
следующего кодового слова.
3. Свойство отсутствия префикса.
Достаточным (но не необходимым) условием того, что код единственным
образом декодируемый, является то, что никакое кодовое слово не
является префиксом другого кодового слова. Коды, удовлетворяющие
этому условию, называются кодами свободными от префикса или префиксными
кодами.