As mentioned above all database objects (components) are stored in the Access database as a single file. It means that MS Access is a file/server-based database. Unlike client-server RDBMS, MS Access does not implement database triggers, stored procedure, or transaction logging.
A file/server is a computer attached to a network that has the primary purpose of providing a location for the shared storage of computer files. A file/server does not usually perform any calculations, and does not run any programs on behalf of the clients. It is designed primarily to enable the rapid storage and retrieval of data where the heavy computation is provided by the workstations. But file/servers frequently run up against performance bottlenecks that limit the speed at which data can be passed to and from the network clients.

Split database architecture

Microsoft Access applications can adopt a split database architecture. The database can be divided into a front end database that contains the application objects (queries, forms, reports, macros, and modules) and is linked to tables stored in a “back end” shared database containing the data. The “back-end” database can be stored in a location shared by many users, such as a file server. The “front-end” database is distributed to each user's desktop and linked to the shared database. Using this design, each user has a copy of Microsoft Access installed on this machine along with the application database. It reduces network traffic since the application is not retrieved for each use, and allows the front end database to contain tables with data that is private to each user for storing settings or temporary data. This split database design also allows development of the application without dependency on the data. When a new version is ready, the “front end” database is replaced without impacting the data database. Microsoft Access has two built-in utilities, Database Splitter and Linked Table Manager, to facilitate this architecture.

Database design

The "right" way to a design database is to make a clean logical design first, and then, as a separate and subsequent step, to map the logical design into whatever physical structures the target DBMS happens to support. Brief review of basic terms of database design theory:

1. Functional dependencies

A functional dependency (FD) is a constraint between two sets of attributes in a relational database. Given a relation R, a set of attributes X in R is said to functionally determine another attribute Y, also in R,(written X→Y) if and only if each X value is associated with precisely one Y value. Usually we call X the determinant set and Y the dependent attribute. Thus when given tuple and the values of the attributes in X, one can determine the corresponding value of the Y attribute. For the purposes of simplicity, let X and Y be sets of attributes in R, X → Y denote that X functionally determines each of the members of Y. In this case Y is known as the dependent set. Thus, a candidate key is a minimal set of attributes that functionally determine all of the attributes in the relation.
A functional dependency FD: X → Y is called trivial if Y is a subset of X.

2. Armstrong’s axioms
Armstrong’s axioms are a set of inference rules used to infer all the FDs on a relational database (RDB). These axioms are used for generating only FDs in the closure of a set of FDs (denoted as F+) when applied to that set (denoted as F). All FDs in the closure F+ define all the other possible FDs for this relation.
Let R(U) be a relation scheme over the set of attributes U. Henceforth we will denote by letters A, B, C, D any subset of U and, for short, the union of two sets of attributes A and B by AB instead of the usual A B:

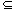
• Axiom of reflexivity: (B A) ═> (A→ B);
• Axiom of augmentation: (A → B) ═> (AС→ BС);
• Axiom of transitivity: (A → B) ^ (B→ C)═> (A →C);
• Self-determination: A A;
• Decomposition: (A → BС) ═> (A→ B) (A → С);
• Union: (A → B)^ (A → С)═> (A → BС);
• Composition: (A→ B)^ (C→ D)═> (AC → BD);
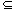
• Darwen’s GUT: (A → B)^ (С → D)═> (А (С – B)→ BD ).

• Example 1: Darwen’s «General Unification Theorem» proof This proof is answer on exercise number 11.5 from Date’s book [1]. Given: (A → B) and (С→ D).
Proof:

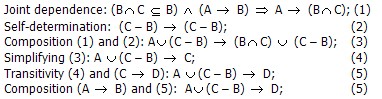
This completes the proof.
3. Closure of a set of FDs and closure of a set of attributes
The set of all FDs that are implied by a given set S of FDs is called the closure of S and written S+.
Example 2: Closure of FDs Suppose we are given a relvar (relational variable) R with attributes A, B, C, D, E, F and the FDs: A→ BC, B → E, CD → EF. Show that the FD AD→ F holds for R and is thus a member of the closure of the given set:
1. A→ BC (given)
2. A → C (decomposition for 1)
3. AD → CD (augmentation for 2)
4. CD→ EF (given)
5. AD→ EF (transitivity for 3 and 4)
6. AD→ F (decomposition for 5)

The completion of a finite set of attributes X under a finite set of FDs S, written as X + , is the smallest superset of X such that:
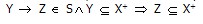Example 3: Computing the closure of the set attributes. Suppose we are given a relvar R with attributes A, B, C, D, E, F, and FDs: S = {A → BC, E → CF, B → E, CD → EF}. Now compute the closure {A,B}+ of set attributes {A,B} under S.
1. Initialize result set to {A,B} (hereinafter in this section referred to as «CLOSURE»).
2. Look at the first FD: we add attribute C (and B) to CLOSURE because the left side is indeed a subset of CLOSURE and CLOSURE is now the set {A, B, C}.
3. The left side of second FD is not a subset of the CLOSURE.
4. The left side of third FD is indeed a subset of CLOSURE and CLOSURE is now the set {A, B, C, E}.
5. The left side of fourth FD is not a subset of the CLOSURE and CLOSURE remains unchanged.
6. Now we go round the inner loop four times again. On the first FD, the result does not change; on the second, it expands to {A, B, C, E, F}; on the third and fourth, it does not change.
7. Change stop for CLOSURE. By this is meant that process terminate and also that {A, B}+ = {A, B, C, E, F}.

Given a set S of FDs, we can easily tell whether a specific FD X → Y follows from S, as FD will follow if and only if Y is a subset of the closure X+ of X under S. In other words. we have a simple way of determining whether a given FD X → Y is in the closure S+ of S, without actually having to compute the closure S+.
            4. Algorithm to derive candidate keys from functional dependencies
       INPUT: a set S of FDs that contain only subsets of a header H
       OUTPUT: the set C of superkeys that hold as candidate keys in
                         all relation universes over H in which all FDs in S hold
       begin