Лабораторная работа № 5

Построение и исследование
математических моделей объектов управления

Цель работы: освоение и практическое применение методов аналитического построения математических моделей (ММ) простейших типовых объектов управления (ОУ). Освоение и практическое применение методов расчёта и имитационного моделирования динамических объектов.

Программа работы
1. Аналитическое построение математической модели буферной ёмкости как ОУ уровня, с использованием расчётной схемы и концептуальной модели, по варианту задания (табл.1).
2. Расчёт параметров ММ условного ОУ по численным значениям исходных данных (расчёт производится в среде MathCAD).
3. Разработка имитационной модели ОУ в среде Simulink приложения MATLAB.
4. Исследование имитационной модели ОУ с иллюстрацией результатов фрагментами проекта в среде Simulink.
5. Выводы.

Исходные данные

Объектом исследования является буферная ёмкость технологического процесса, рассматриваемая как ОУ уровнем, который является мерой запаса вещества в ёмкости.
Концептуальная модель буферной ёмкости (рис.1) представляет собой цилиндрический аппарат, для которого заданы высота и диаметр (или площадь зеркала), а также номинальное значение уровня хранимой в нём жидкости. Ёмкость имеет входной и выходной патрубки.
Входной патрубок через регулирующий орган соединён с подключаемым питающим коллектором.
Запасаемая жидкость под давлением P_K через регулирующий орган с условной проводимостью a₁ поступает в буферную ёмкость, преодолевая гидростатическое давление столба жидкости, запасённой в ёмкости. Отмеряемые от дна высота ввода входного патрубка ёмкости , выходного .
Поток отводимой жидкости через второй регулирующий орган с условной проводимостью  свободно вытекает под действием гидростатического напора в расположенный ниже накопительный резервуар.

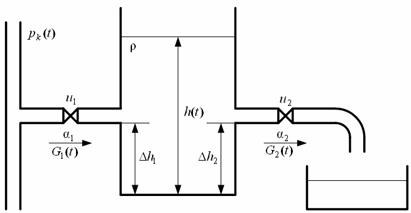Рис. 1. Концептуальная модель буферной ёмкости

Ёмкость характеризуется площадью зеркала , жидкость характеризуется удельной массой (плотностью) p.
Расход жидкости через регулирующий орган зависит от разности давлений до и после регулирующего органа  , от условной проводимости регулирующего органа  и от степени открытия регулирующего органа , которая является управляющим воздействием. Значение  принимается нормированным в диапазоне {0,1}, т.е. .
Выражение ММ: .
Для расчёта параметров ММ необходимо построить программу расчёта в пакете математического моделирования, например в Mathcad или MatLab.

Указания к проведению работы

При построении ММ любого ОУ рекомендуется действовать следующим образом:

1. Определить выходы ОУ – ими являются те значения, которые необходимо регулировать.
2. Определить входы ОУ – величины, которые будут изменяться непосредственно управляющим устройством и влиять на регулируемую величину.
3. Определить возмущения, действующие на объект – входные параметры, чьё изменение происходит «извне», но которые также влияют на регулируемую величину.
4. Двигаясь от выхода к входам, определить структуру модели.
5. Определить параметры каждого блока.

Для расчёта индивидуальных параметров каждого варианта необходимо задать ряд исходных значений переменных и констант, а по ним рассчитать недостающие. К исходным константам относятся: конструктивные параметры аппарата  и  и его технологическая константа  – номинал уровня. Последовательность действий:
1) Задаться .
2) По заданным  и  рассчитать номинальный перепад давления на первом регулирующем органе путём задания номинального давления в коллекторе , которое должно быть значительно больше, чем противодавление.
3) Рассчитать номинальный гидростатический напор:
,
давление столба жидкости на выходной патрубок.
4) Положение регулирующих органов при номинальном режиме работы соответственно u₁₀ и u₂₀. Поскольку номинальный режим работы строится из условия изменения положения уровня как в положительную, так и в отрицательную сторону, номинальные значения управлений должны находиться приблизительно в середине диапазона 0,4 – 0,6: .
5) Последним этапом расчёта параметров условного ОУ является выбор номинального значения расхода жидкости, протекающей через буферную ёмкость, и вычисление значений , обеспечивающих такой расход. Расчёт производится из условий выполнения закона сохранения. Поскольку в номинальном невозмущённом режиме работы справедлива статическая модель закона сохранения, которая для данного объекта сводится к равенству прихода и расхода, то ММ статики для буферной ёмкости: .
Величина  выбирается следующим образом: поскольку назначением буферной ёмкости является создание запаса жидкости, то технической характеристикой этого свойства является условное время опорожнения, т.е. время, за которое истощится запас жидкости в ёмкости при отсутствии подпитки из коллектора при номинальном расходе. Это время рассчитывается по формуле
 или .
Таким образом,  можно рассчитать по формуле , где t – время опорожнения. Рассчитав номинальное значение , можно рассчитать  и  по выражению .
После расчёта параметров модели необходимо провести исследование модели в пакете Simulink, обращая при этом внимание на фактическое время расхода воды из ёмкости, максимально допустимом уровне, и т.д.

Варианты заданий
Таблица 1