Лабораторная работа № 2

Исследование фундаментальных свойств
замкнутых автоматических систем

Цели работы: 1) показать достоинства и недостатки замкнутого принципа управления по отклонению, 2) оценить качественное изменение системы после замыкания обратной связи, 3) на примере замкнутой САУ наглядно показать переход количественных изменений в качество.
Программа работы
1.     Ознакомиться с основными приёмами работы в программе для моделирования САУ Classic 3:
1.1. Формирование проекта отдельного динамического звена.
1.2. Ввод и изменение его параметров.
1.3. Проведение связей между блоками.
1.4. Назначение «входов» и «выходов» модели.
1.5. Построение характеристик моделируемой системы.
2.     Построить модель замкнутой системы, состоящей из П-регулятора, ОУ в виде двух типовых звеньев второго порядка и единичной обратной связи, ввести параметры модели в соответствии с вариантом задания.
3.     Определить зависимость количественных оценок качественного изменения ПП САУ от величины коэффициента П-регулятора. Для этого:
3.1. Установить начальное значение k_П = 1 и снять характеристики модели САУ. Результаты занести в таблицу вида табл.1.
3.2. Увеличивая k_П , определить, при каком значении k_П^a-k переходный процесс системы вместо апериодического вида примет колебательный характер. Зафиксировать данное значение коэффициента, отразить его в таблице результатов, снять характеристики САУ при k_П^a-k.
3.3. При дальнейшем варьировании k_П, переходный процесс системы будет принимать всё более ярко выраженный колебательный характер. Необходимо отразить это на графиках переходных процессов замкнутой САУ при соответствующих значениях k_П.

Результаты опыта
Таблица 1

3.4. По достижении некоторой величины k_П^к-н, переходная характеристика замкнутой системы управления станет близкой к автоколебательному виду, а затем (после превышения данного порогового значения k_П=k_П^к-н) замкнутая система станет неустойчивой. Определить означенное выше пороговое значение k_П^к-н, снять основные показатели качества замкнутой САУ (табл.1).
4. Отразить изменения характера переходных процессов модели замкнутой САУ при соответствующих значениях k_П на графиках зависимостей:

5. Сформулировать выводы о проделанной работе: определить порядок астатизма системы, применимость П-регулятора для исследуемой системы, и т.д.

Указания к выполнению работы

К п.2. Возможный вид структурной схемы модели выглядит так, как показано на рис.1а и 1б. Здесь блок 1 является П-регулятором, блоки 2 и 3 – составляющие объекта управления ОУ1 и ОУ2, блок 4 – звено единичной обратной связи.

а

б

Рис.1. Схема исследуемой модели:
а – для получения переходного процесса,
б – для получения ошибки регулирования.

Передаточные функции блоков №2 «ОУ 1» и №3 «ОУ 2» для упрощения процедуры ввода параметров приведены в следующей форме:
, .

Значения C₁, C₂, C₃, C₄, C₅, C₆ выбираются из таблицы 2 согласно номеру варианта задания.
К п.3. Варьировать значение коэффициента П-регулятора следует в параметрах блока 1, а точнее – в числителе его передаточной функции (см. рис.2).

  
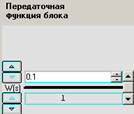
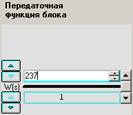
Рис.2. Варьирование коэффициента обратной связи

Необходимо обращать внимание на тип переходного процесса. При различных вариантах заданий и значениях k_П  он может быть и апериодическим (как с небольшим перерегулированием, так и без него), и колебательным; при некотором значении k_П  система станет неустойчивой. Необходимо определить, при каких значениях k_П  происходят качественные перемены свойств САУ, и зафиксировать значения её показателей качества в таблице 1.
Прямые показатели качества модели замкнутой САУ можно определить по графику «Переходные процессы»: это перерегулирование и время регулирования, а также установившееся значение регулируемой величины. Делается это нажатием ПКМ на окне графика «Переходные процессы» и выбором пункта контекстного меню «Показатели качества (сводка)».

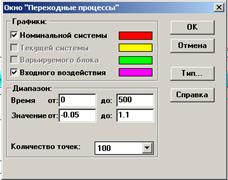Рис.3. Окно свойств графика переходного процесса

В случае, если необходимо изменить масштаб графика, следует изменить максимальные значения осей графиков в окне «Переходные процессы», в поле «Диапазон» (рис.3). Вызвать его можно следующим образом: клик ПКМ на графике «Переходные процессы»/пункт меню «Параметры…».
Характеристический полином (ХП) рассматриваемой системы будет иметь три корня, один из которых всегда принимает вещественное значение, а два других – комплексно сопряжённые: .
Корни ХП модели определяются по графику «Корневая плоскость» аналогичным способом.
Показатель колебательности следует определять по отношению мнимой  части комплексного корня к его действительной составляющей следующим образом: .
К п.4. В результате исследования модели в таблицу 1 заносятся как прямые показатели качества переходного процесса модели САУ, так и значения корней её ХП. На основании полученных данных необходимо проследить связь между изменениями коэффициента передачи звена обратной связи (k_П ) и основных показателей качества системы.

Варианты заданий
Таблица 2

.