|
Тема
№7.
Показательные
уравнения.
7.2. Классификация показательных уравнений.
1.
Уравнения, решаемые
переходом к одному основанию.
Пример
18. Решить
уравнение  . .
Решение:
Воспользуемся тем, что все
основания степеней являются
степенями
числа 5:
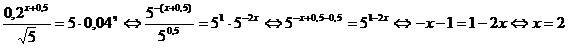 . .
2.
Уравнения, решаемые
переходом к одному
показателю степени.
Эти
уравнения решаются преобразованием исходного уравнения к виду
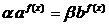 ,
которое использованием свойства пропорции приводится к
простейшему. ,
которое использованием свойства пропорции приводится к
простейшему.
Пример 19. Решить
уравнение: 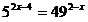
Решение:
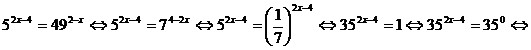
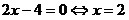 . .
3.
Уравнения,
решаемые вынесением общего
множителя за скобки.
Если в уравнении
каждый показатель
степени отличается от другого
на некоторое число,
то уравнения решаются
вынесением за скобки
степени с наименьшим
показателем.
Пример
20. Решить уравнение 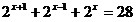 . .
Решение:
Вынесем в левой части уравнения степень с наименьшим
показателем за
скобки:
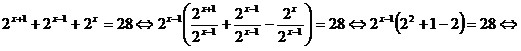
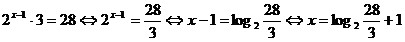 . .
Пример
21. Решить уравнение 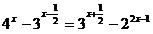
Решение:
Сгруппируем отдельно в левой части уравнения слагаемые,
содержащие
степени с
основанием 4, в правой части – с основанием 3, затем
вынесем степени с
наименьшим показателем за скобки:
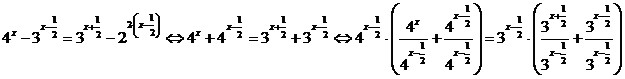
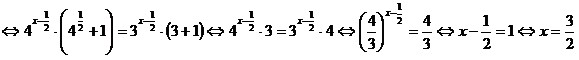 . .
4.
Уравнения,
сводящиеся к квадратным (или
кубическим) уравнениям.
К квадратному
уравнению относительно
новой переменной y
сводятся
уравнения:
а) вида 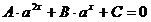 подстановкой подстановкой 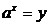 , при
этом , при
этом 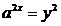 ; ;
б) вида 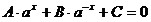 подстановкой подстановкой 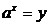 , при
этом , при
этом 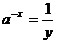 . .
Пример
22. Решить уравнение 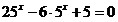 . .
Решение:
Сделаем замену переменной 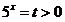 и решим квадратное и решим квадратное
уравнение:
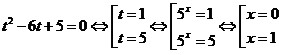 . .
Ответ: 0; 1.
5.
Однородные относительно
показательных функций уравнения.
Уравнение
вида 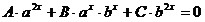 является однородным является однородным
уравнением второй
степени относительно
неизвестных ax
и bx
.
Такие
уравнения сводятся
предварительным делением обеих частей на 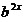 и и
последующей
подстановкой
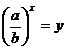 к квадратным
уравнениям. к квадратным
уравнениям.
Пример
23. Решить уравнение 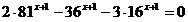 . .
Решение:
Разделим обе части уравнения на 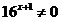 : :
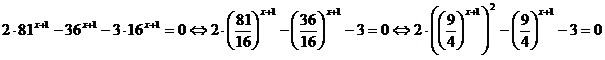 . .
Положив 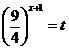 ,
получим квадратное уравнение ,
получим квадратное уравнение 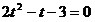
с корнями 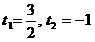 . .
Теперь задача
сводится к решению
совокупности уравнений
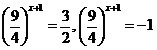 . Из
первого уравнения находим, что . Из
первого уравнения находим, что 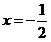 . .
Второе уравнение не
имеет корней, так как 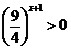 при любых значения x. при любых значения x.
Ответ: -1/2.
6.
Рациональные
относительно показательных
функций уравнения.
Пример
24. Решить уравнение 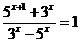 . .
Решение:
Разделим числитель и знаменатель дроби на 3x и
получим вместо двух
– одну показательную функцию:
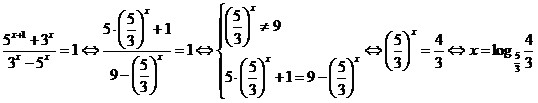
7.
Уравнения вида 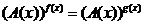 . .
Такие
уравнения с множеством допустимых значений (ОДЗ),
определяемым
условием 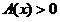 ,
логарифмированием обеих ,
логарифмированием обеих
частей уравнения
приводятся к
равносильному
уравнению 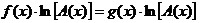 ,
которые в свою очередь ,
которые в свою очередь
равносильны
совокупности двух
уравнений 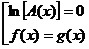
или
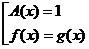 . .
Пример
25. Решить уравнение: 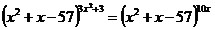 . .
Решение:
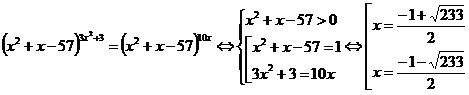 . .
Дидактический
материал.
Решите
уравнения:
1.
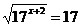 ; 2. ; 2. 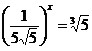 ;
3. ;
3. 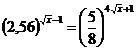 ; ;
4. 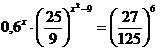 ; 5. ; 5.
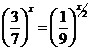 ;
6. ;
6.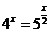 ; ;
7. 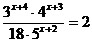 ; 8. ; 8. 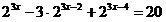 ; ;
9. 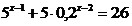 ; 10. ; 10.
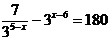 ;
11. ;
11. 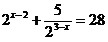 ; ;
12. 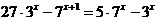 ; 13. ; 13. 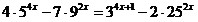 ; ;
14. 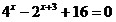 ;
15. ;
15.
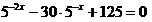 ; ;
16. 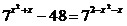 ; 17. ; 17.
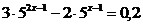 ; ;
18. 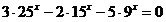 ;
19. ;
19. 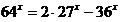 ; ;
20. 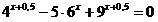 ; 21. ; 21.
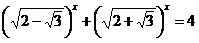 ; ;
22. 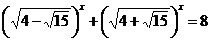 ;
23. ;
23. 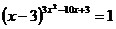 ; ;
24. 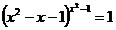 ;
25. ;
25. 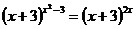 . .
26. Найдите
произведение корней
уравнения 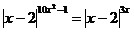 . .
27. Найдите сумму
корней
уравнения 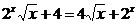 . .
Найдите значение
выражения:
28. 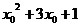 , где x0
– корень уравнения , где x0
– корень уравнения 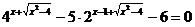 ; ;
29. 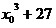 , где x0
– целый корень
уравнения , где x0
– целый корень
уравнения 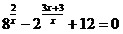 . .
Решите уравнение:
30. 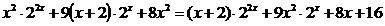 ; ;
31. 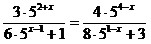 ; 32. ; 32.
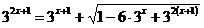 . .
Ответы: 1. 0; 2. -2/9; 3. 1/36; 4. 0,
0.5; 5. 0; 6. 0; 7. -2; 8. 2;
9. 1, 3; 10. 8;
11.
5; 12. 1; 13. ¼; 14. 2; 15. -2, -1; 16. -2, 1; 17. 0; 18.
1; 19. 0; 20. -1, 0;
21.
-2, 2; 22. -2, 2; 23. 4; 24. -1, 2; 25. -2, -1, 3; 26.
-0.3; 27. 3; 28. 11; 29.
54;
30. -1, 0, 2, 3; 31. 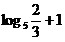 ;
32. ;
32. 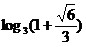 . .
|
