|
Тема
№5.
Неравенства
с одной переменной (часть II).
5.2. Множество значений функции.
1º. Множеством (областью) значений E(y) функции y=f(x) называется
множество всех таких чисел y0, для
каждого из которых найдется число x0 такое, что f(x0)=y0.
2º. Областью значений всякого многочлена четной степени является
промежуток 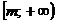 , где m – наименьшее
значение этого многочлена, либо промежуток , где m – наименьшее
значение этого многочлена, либо промежуток 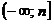 , где n – наибольшее
значение этого многочлена. , где n – наибольшее
значение этого многочлена.
Областью значений всякого многочлена нечетной степени является R.
3º. Области значений основных элементарных
функций:
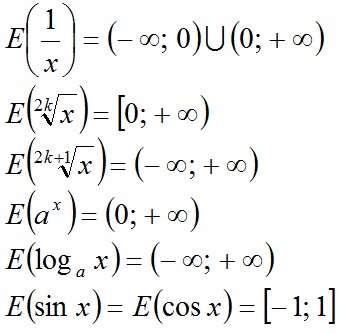
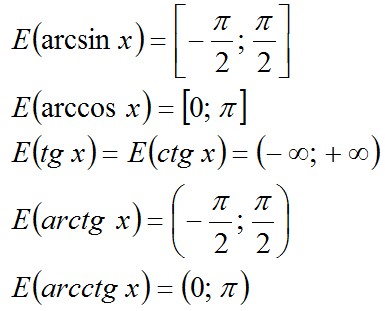
Пример 15.
Найти множество значений функции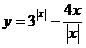 , если x≤1. , если x≤1.
Решение: Данная функция не определена при x=0 и,
следовательно, задана на множестве 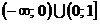 . .
Рассмотрим x<0, тогда |x|=-x и функция принимает вид 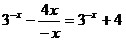 . Так как . Так как 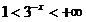 для x<0, то для x<0, то 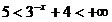 . Таким образом, на промежутке . Таким образом, на промежутке 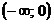 функция принимает
значения от 5 до +∞. функция принимает
значения от 5 до +∞.
Если x>0, то |x|=x и функция имеет вид 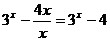 . Так как . Так как 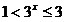 для для 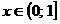 , то , то 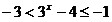 . .
Ответ: 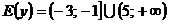 . .
Дидактический
материал.
Решите неравенства:
1. 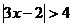 ; 2. ; 2.
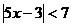 ;
3. ;
3.
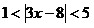 ; ;
4. 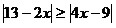 ; 5. ; 5. 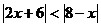 ; 6. ; 6. 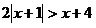 ; ;
7. 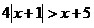 ; 8. ; 8. 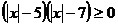 ; 9. ; 9. 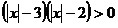 ; ;
10. 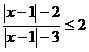 ; 11. ; 11. 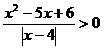 ; 12. ; 12. 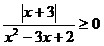 ; ;
13. 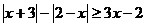 ;
14. ;
14.
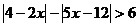 ; ;
15. 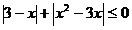 ;
16. ;
16.
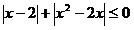 ; ;
17. 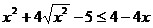 ;
18. ;
18.
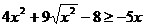 . .
19. При каких
x точки графика функции 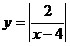 лежат выше лежат выше
прямой 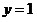 ? ?
20. При каких
x точки графика 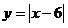 лежат не ниже точек
графика функции лежат не ниже точек
графика функции 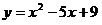 ? ?
Найти
множество значений функции:
21. 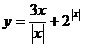 , если , если 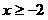 ; 22. ; 22.
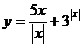 , если , если 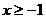 . .
|
