|
Тема №5.
Неравенства
с одной переменной (часть II).
5.1.
Неравенства, содержащие знак модуля.
1º. При
решении неравенств,
содержащих неизвестные под знаком
модуля,
используется определение модуля, что
приводит
к
рассмотрению двух случаев:
а)
f(x) ≥ 0,
тогда |f(x)|
= f(x);
б)
f(x)<0,
тогда |f(x)|
= -f(x).
2º.
При решении неравенств вида |f(x)|
< a
или |f(x)|
> b полезно
использовать
следующие соотношения:
1)
неравенство вида |f(x)|
< a (или
|f(x)|
≤ a),
где a
> 0,
равносильно
двойному неравенству –a
< f(x) < a
(или –a
≤ f(x) ≤ a);
2)
неравенство вида |f(x)|
> b (или |f(x)|
≥ b), где b > 0, равносильно
совокупности
двух неравенств 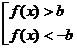
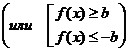 . .
3º.
Для решения неравенств вида |f(x)|
> |g(x)|
используют метод
возведения
в квадрат обеих частей
неравенства:
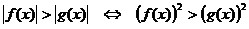
Пример
13.
Решить неравенство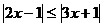 .
.
Решение:
Возведя обе части неравенства в квадрат,
получим
неравенство,
равносильное данному: 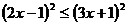 . .
Преобразовав
последнее неравенство, получим 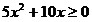 , ,
откуда
находим: x
≤ - 2 , x ≥ 0.
Ответ:
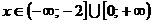 . .
4º.
Для решения неравенств вида
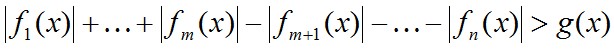 часто применяют часто применяют
«метод
промежутков». Находят ОДЗ неравенства, затем находят
корни
совокупности
уравнений 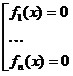 . .
Эти корни
разбивают ОДЗ на некоторое число промежутков.
На каждом
промежутке |fi(x)|=fi(x)
или |fi(x)|=-fi(x),
i=1,2,…,n.
Поэтому
на
каждом из них данное
неравенство заменяется на другое
неравенство, уже не
содержащее знаков модуля и равносильное
данному неравенству
на этом промежутке.
Затем решают полученные
неравенства (каждое
на своем промежутке). Объединение всех
найденных
решений дает решение
исходного неравенства.
Пример 14. Решить неравенство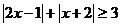 . .
Решение:
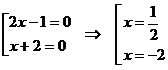
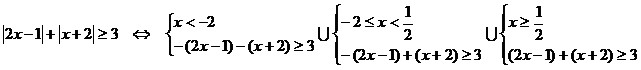
Решение
первой системы: 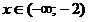 ;
второй: ;
второй: 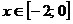 ;
третьей: ;
третьей:
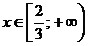 .
Объединяя, получим .
Объединяя, получим 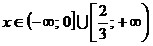 . .
|
