|
Тема
№4.
Неравенства
с одной переменной (часть I).
4.1. Решение линейных и квадратных
неравенств.
1º. Решить
неравенство с одной переменной – значит найти
множество
значений переменной, при которых это неравенство является верным.
Элементы
этого множества называются решениями
неравенства.
Два
неравенства, содержащие одну и ту же переменную, называются равносильными, если множества решений
этих неравенств совпадают. Равносильность неравенств обозначается так: 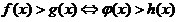 . .
2º.
Линейным неравенством
называется неравенство вида
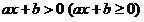 ,
где ,
где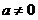 . .
Если a > 0,
то
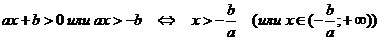
Если a < 0,
то 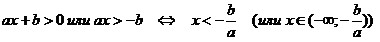 .
Пример 9. Решить неравенство,
сводящееся к линейному:
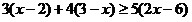 . .
Решение:
Раскрыв скобки, получим:
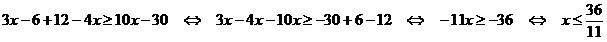 .
Ответ: 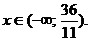
3º. Квадратным
неравенством называется неравенство вида 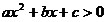 (или (или
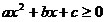 ),
где а ≠ 0. ),
где а ≠ 0.
При
решении квадратного неравенства 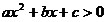 в зависимости от знака
дискриминанта в зависимости от знака
дискриминанта 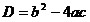 могут представиться 3
варианта: могут представиться 3
варианта:
1) Если D
< 0, то график квадратного
трехчлена 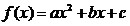 не пересекает ось Ох и лежит выше этой оси при a
> 0 и ниже ее при a < 0.
В первом случае
множество решений неравенства есть вся числовая прямая, а во втором
– пустое
множество. не пересекает ось Ох и лежит выше этой оси при a
> 0 и ниже ее при a < 0.
В первом случае
множество решений неравенства есть вся числовая прямая, а во втором
– пустое
множество.
2) Если D
> 0, то график квадратного
трехчлена пересекает ось Ох в
точках х1 и х2 (x1
< x2),
являющихся корнями уравнения 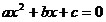 .
Эти точки разбивают числовую прямую на три промежутка (-∞;
x1), (x1;
x2), .
Эти точки разбивают числовую прямую на три промежутка (-∞;
x1), (x1;
x2),
(x2;
+∞). Если a > 0,
то решением
неравенства является множество 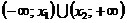 .
Если a
< 0, то решением
неравенства является множество (x1;
x2). .
Если a
< 0, то решением
неравенства является множество (x1;
x2).
3) Если D
= 0, то график квадратного
трехчлена касается оси Ох в точке х1, являющейся
единственным
корнем уравнения 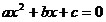 .
При a
< 0 решением неравенства будет
пустое множество, при a > 0 –
множество . .
При a
< 0 решением неравенства будет
пустое множество, при a > 0 –
множество .
Пример 10.
Решить неравенство 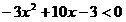 . .
Решение:
Рассмотрим функцию 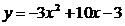 .
Графиком этой функции является парабола, ветви которой
направлены вниз, так как a = -3 < 0. .
Графиком этой функции является парабола, ветви которой
направлены вниз, так как a = -3 < 0.
Решим
уравнение 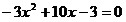 или или 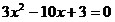 .
Корни этого уравнения .
Корни этого уравнения 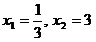 .
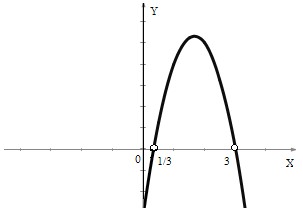
Изобразив схематически параболу .
Изобразив схематически параболу
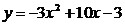 ,
найдем, что y < 0 в каждом из промежутков
(-∞; 1/3), (3; +∞). ,
найдем, что y < 0 в каждом из промежутков
(-∞; 1/3), (3; +∞).
Ответ: 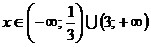 . .
|
