|
Тема №3.
Степени
и корни.
3.2. Арифметический корень. Степень с рациональным
показателем.
1º. Арифметическим корнем k-ой степени (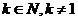 ) из числа ) из числа
а ≥ 0 называется неотрицательное число b, k-ая степень которого равна а:
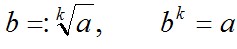
2º. Замечание. Для любого действительного числа а,
любого натурального числа n действуют правила:
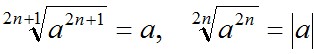 в частности в частности 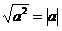 . .
3º. Свойства арифметических корней. Пусть 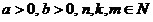
Тогда:
1) 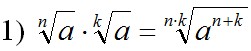 ; 2) ; 2) 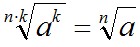 ; 3) ; 3) 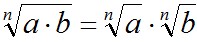 ; ;
4) 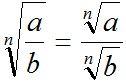 ;
5) ;
5)
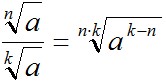 ; 6) ; 6) 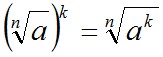 ; ;
7) 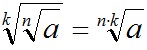 . .
4º. Степенью числа a с рациональным показателем 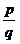
определяется равенством:
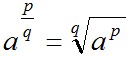
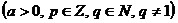
Степень с рациональным показателем
обладает теми же свойствами,
что и степень с целым показателем.
Пример
7. Упростить выражение: 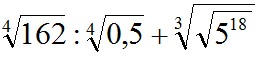 . .
Решение.
Используя определение степени и ее свойства, получим:
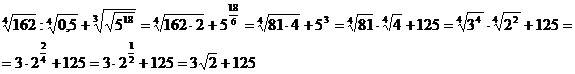
|
