Уравнения. Модуль числа

              2.4. Квадратичная функция, ее график.

1º. Функция, заданная формулой ,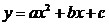 
где x, y – переменные, a, b, c –  действительные числа, причем а ≠ 0, 
называется квадратичной

2º. Графиком функции 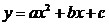 является парабола – кривая,симметричная относительно прямой 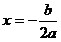,проходящей через вершину параболы.

Координаты вершины параболы определяются по формулам:

.

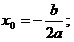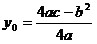Если квадратичную функцию 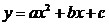 путем выделения 
полного квадрата привести к виду

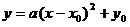, то точка (x₀; y₀) – вершина параболы.
График квадратичной функции

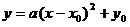  получается из графика функции 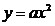 с помощью параллельного переноса.

3º. Если коэффициент a > 0, ветви параболы направлены вверх,если a < 0 – вниз.
При 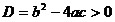 парабола пересекает ось абсцисс в двух точках, 
при D=0 – в одной (т.е. касается оси Ох), при D<0 - парабола не 
пересекает ось абсцисс.
Пример 3. Построим график функции  .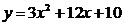

         Выполним следующие преобразования 
              (называемые «выделением полногоквадрата»):

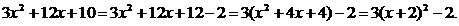
График функции 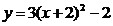 получается из графика функции 

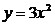 параллельным переносом на 2 единицы влево и на две единицы вниз.