Тема №2.

 Уравнения. Модуль числа.

    2.3.Квадратные уравнения.

1º. Уравнение вида 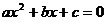, где a,b,c – действительные числа, 

причем а ≠ 0, называют квадратным уравнением.

Корни квадратного уравнения 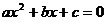 находят по формуле:

.

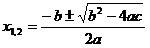Если коэффициент а = 1, то квадратное уравнение называют приведенным; 

если коэффициент а ≠ 1 – неприведенным.

2º. Выражение 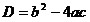 называют дискриминантом квадратного уравнения.

Если D < 0, то уравнение 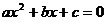    не имеет действительных корней; 

если D = 0, то уравнение имеет один действительный корень 

(или два одинаковых корня); если D > 0, уравнение имеет два различных 

действительных корня.

3º. Теорема Виета. Сумма корней квадратного уравнения  

равна 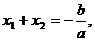  а произведение корней равно .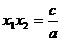

Для корней x₁ и x₂ приведенного квадратного уравнения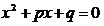  

формулы Виета имеют вид: 

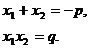
4º. Уравнения вида 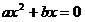, , 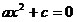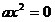-называют неполными квадратными уравнениями.

Неполные квадратные уравнения решают следующим образом:

1) ;

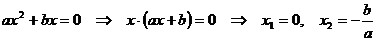2) 

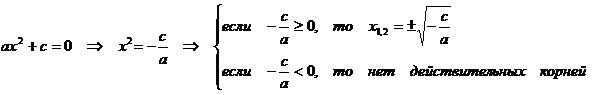
5º. Выражение 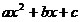  называется квадратным трехчленом 

относительно х.

            Квадратный трехчлен 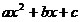 может быть разложен на линейные 

множители по формуле:

,

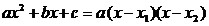где x₁ и x₂ – корни квадратного трехчлена, т.е. корни уравнения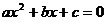  (если уравнение имеет действительные корни).