|
Тема №12.
Решение
геометрических задач.
12.1.Планиметрия.
1º.
Произвольный треугольник.
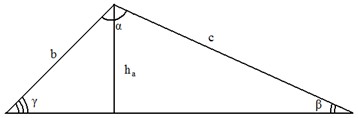
a,
b, c
– стороны;
α, β, γ
– противолежащие им
углы;
p
– полупериметр;
R
– радиус описанной окружности;
r
– радиус вписанной окружности;
S – площадь;
ha
– высота, проведенная к стороне a.
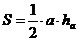 ; ;
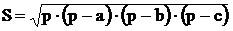 (формула Герона); (формула Герона);
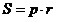 ; ;
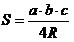 ; ;
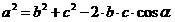 (теорема косинусов); (теорема косинусов);
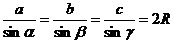 (теорема синусов). (теорема синусов).
Следует
иметь в виду, что:
1) центр
окружности, вписанной в треугольник, находится в точке
пересечения биссектрис
треугольника;
2) центр
окружности, описанной около треугольника, находится в
точке пересечения
серединных перпендикуляров сторон треугольника;
3) медианы
треугольника пересекаются в одной точке, которая делит
каждую медиану в
отношении 2:1, считая от вершины.
2º.
Прямоугольный треугольник.
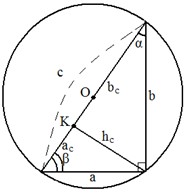
a,
b – катеты; c
– гипотенуза;
ac,
bc – проекции катетов на
гипотенузу;
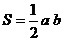 ; ;
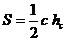 ; ;
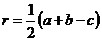 ; ;
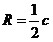 (центр описанной
окружности находится на середине (центр описанной
окружности находится на середине
гипотенузы);
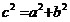 (теорема Пифагора); (теорема Пифагора);
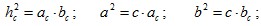
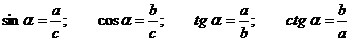 . .
3º.
Равносторонний треугольник.
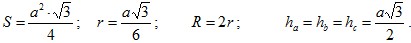
4º.
Параллелограмм.
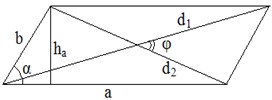
a, b
– смежные стороны;
α
– угол между ними;
d1
и d2
–
диагонали;
φ
– угол между диагоналями;
ha
– высота, проведенная к стороне a;
S
– площадь.
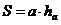 ; ;
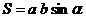 ; ;
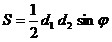 ; ;
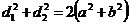 (сумма квадратов
диагоналей параллелограмма (сумма квадратов
диагоналей параллелограмма
равна
сумме квадратов всех его сторон).
5º.
Ромб.
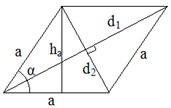
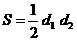 ; ;
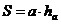 ; ;
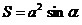 ; ;
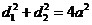 . .
6º.
Прямоугольник.
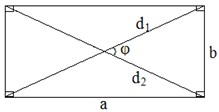
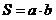 ; ;
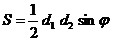 ; ;
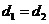 . .
7º.
Квадрат.
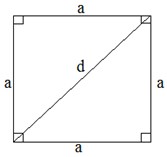
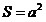 ; ;
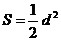 . .
8º.
Трапеция.
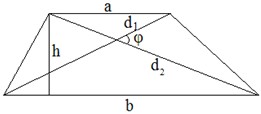
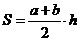 ; ;
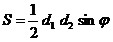 . .
9º.
Описанный многоугольник.
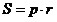 , ,
где p
– полупериметр, r
–
радиус вписанной окружности.
10º.
Правильный многоугольник.
Если an
– сторона правильного n-угольника,
R –
радиус
описанной
окружности, r
– радиус
вписанной окружности, то:
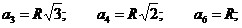
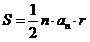 . .
11º.
Окружность, круг.
Если r
– радиус, C
– длина окружности, S -
площадь круга, то:
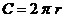 ; ;
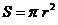 . .
Пример 46. В прямоугольном
треугольнике медианы катетов равны
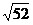 и и 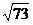 .
Тогда гипотенуза треугольника равна: .
Тогда гипотенуза треугольника равна:
1) 8
2) 12
3) 10
4)
14
5) 16.
Решение.
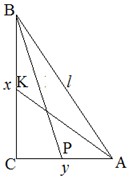 Введем следующие обозначения:
Введем следующие обозначения:
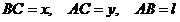 . Тогда
по теореме . Тогда
по теореме
Пифагора получаем:
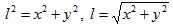 , ,
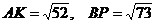 . .
По условию задачи: 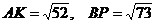 . .
1) Из ΔBPC:
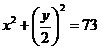 , , 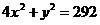 . (1) . (1)
2) Из ΔAKC:
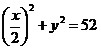 , ,
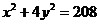 . (2) . (2)
Из (1) и (2)
получаем систему алгебраических уравнений:
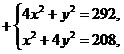
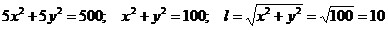 . .
Ответ: 10
(правильный
ответ – №3).
Пример 47. В трапеции сторона
основания равна 7, высота 5,
площадь 25. Тогда
другое основание трапеции равно
1) 6
2) 4
3) 2
4)
3
5) 5.
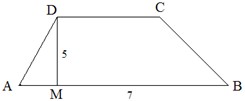 Решение. Решение.
На
рисунке 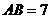 и и
DC
– основания
данной трапеции,
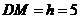 – ее высота
. – ее высота
.
По
условию задачи площадь трапеции равна 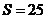 . .
По формуле 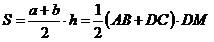 получаем
уравнение получаем
уравнение
относительно DC:
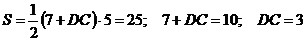 . .
Второе
основание трапеции равно 3.
Ответ: 3 (правильный
ответ – №4).
Пример 48.
Периметр ромба равен 2p см, сумма его диагоналей
равна m см. Тогда площадь ромба равна
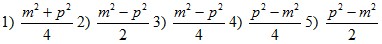
Решение.
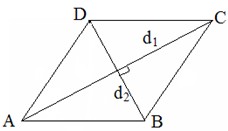 Пусть
дан ромб ABCD, Пусть
дан ромб ABCD,
его диагонали, 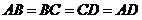 . .
По условию задачи
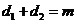 ,
периметр ,
периметр
ромба 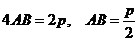 .
Требуется .
Требуется
вычислить площадь
ромба. Площадь ромба вычислим
по формуле 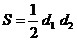 . .
Найдем
произведение диагоналей ромба: 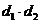 .
Так как сумма .
Так как сумма
квадратов диагоналей
ромба равна сумме
квадратов всех его сторон, то
получаем 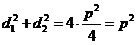 . .
Преобразуем
это равенство: 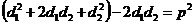 ,
но ,
но 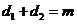 . .
Поэтому 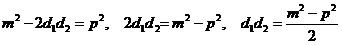 . .
Окончательно, 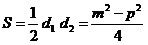 . .
Ответ: 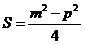 см2
(правильный ответ – №3). см2
(правильный ответ – №3).
Дидактический
материал.
1.
В треугольнике ABC
длины
сторон AB и AC соответственно
равны
4
и 6, а синус угла BAC
равен
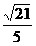 .
Тогда сторона CB
(CB>8)
равна: .
Тогда сторона CB
(CB>8)
равна:
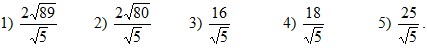
2.
В равнобедренном треугольнике основание равно 18,
а
боковая сторона в
1,25 больше высоты. Тогда площадь
треугольника
равна:
1) 216
2) 108
3) 144
4)
121
5) 110.
3.
В треугольнике сторона, равная 12, расположена против угла
30º.
Тогда
радиус описанной около этого треугольника окружности равен:
1) 24
2) 14
3) 12
4)
8
5) 15.
4.
Около прямоугольника с меньшей стороной, равной 46, и углом
между
диагоналями, равным 60º, описана окружность. Тогда
площадь
круга
равна:
1) 1058π
2) 1600π
3) 2116π
4)
1024π
5) 625π.
5.
В ромб вписана окружность радиуса 2. Определить площадь ромба,
если
его острый угол равен 60º.
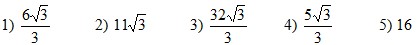
6.
Даны стороны треугольника 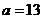 см, см,
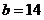 см, см,
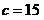 см. см.
Тогда
радиус описанной около него окружности равен:
1) 64
2) 8
3) 7
4) 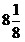 5)
5) 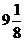
7.
В треугольник вписан круг радиуса 4 см.
Одна
из сторон треугольника
разделена точкой
касания
на части, равные 6 см и 8 см. Тогда длины
двух
других
сторон равны:
1) 13 и 12
2) 12 и 8
3)
13 и 15
4) 11 и 9
5) 10 и 6.
8. Внутри круга, радиус которого
равен 13 см,
дана точка М, отделенная
от центра круга на 5 см. через точку М
проведена хорда 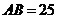 см. Тогда длины
отрезков, на которые хорда AB см. Тогда длины
отрезков, на которые хорда AB
делится
точкой М, равны:
1) 9 и 16
2) 8 и 17
3) 4 и 21
4) 5
и 20
5) 6 и 19
9. Длины катетов прямоугольного
треугольника равны 2 и 3.
Тогда длина
биссектрисы прямого угла этого
треугольника равна:
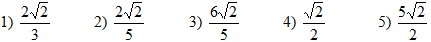
10.
Длины оснований трапеции относятся как 7:3 и различаются на 8.
Тогда
длина средней линии трапеции равна:
1) 6
2) 10
3) 12
4)
8
5) 5.
11. Найти диагональ и боковую
сторону равнобедренной
трапеции с
основаниями 20 см и 12 см, если известно, что
центр
описанной
окружности лежит на большем основании.
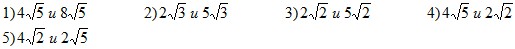
12. Площадь
квадрата, вписанного в
правильный треугольник
со стороной a,
равна:
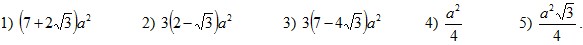
13. Площадь трапеции, параллельные
стороны которой
равны 16 и 44, а
непараллельные – 17 и 25, равна:
1) 420
2) 430
3) 440
4)
450
5) 460
14. Медиана, проведенная к боковой
стороне
равнобедренного
треугольника, делит его периметр на две части,
длины
которых равны 30 и 12 соответственно. Определить длину
основания
треугольника.
1) 1
2) 1,5
3) 2
4)
2,5
5) 3.
15. Сторона ромба равна 16, острый
угол равен 30º.
Определить радиус
вписанного круга.
1) 3
2) 3,5
3) 4
4)
4,5
5) 5.
16. Круг описан около прямоугольного
треугольника,
один из катетов
которого равен 6 см, а угол, лежащий против
этого
катета, равен 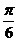 .
Тогда площадь круга равна: .
Тогда площадь круга равна:
1) 6π см2
2) 9π см2
3) 36π см2
4) 144π см2 5)
24π см2
|
