1.2.  Десятичные дроби. Действия над десятичными дробями.

         1º. Обыкновенную дробь со знаменателем 10, 100, 1000 и т.д., записанную без знаменателя, называют десятичной дробью.

      Например, ;       ;          .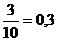

            

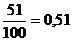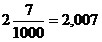                2º. Правила арифметических действий над десятичными дробями:

a)      При сложении (вычитании) десятичных дробей надо записать их одну под другой так, чтобы одинаковые разряды были  друг под другом, а запятая под запятой и сложить (вычесть) их как натуральные числа, не забыв поставить в результате запятую под запятыми.

b)     Чтобы умножить одну десятичную дробь на другую, надо выполнить умножение, не обращая внимания на запятые, и в полученном произведении отделить справа запятой столько цифр, сколько их стоит после запятой в обоих множителях вместе. Если цифр в полученном произведении недостаточно, то приписывают слева нули.

Например, .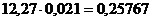

c)    При делении десятичной дроби на натуральное число надо разделить это число, не обращая внимания на запятую, и поставить в частном запятую, когда закончится деление целой части.

Например, .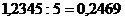

d) Чтобы разделить число на десятичную дробь, нужно в делимом и делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе, а потом выполнить деление на натуральное число. Если в делимом меньше десятичных знаков, чем в делителе, то справа приписывают необходимое количество нулей.

Например, .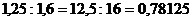

e)При умножении (делении) десятичной дроби на 10,100, 1000 и т.д. достаточно перенести запятую вправо (влево) на столько цифр, сколько нулей во множителе (делителе).

Например, ; .

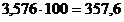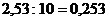3º. При выполнении совместных действий с обыкновенными и десятичными дробями нужно учитывать рациональность выбора: иногда лучше действия выполнить в - обыкновенных дробях, а в других случаях – в десятичных.

a) Любую обыкновенную дробь можно обратить в десятичную (конечную или бесконечную периодическую), разделив числитель на знаменатель по правилу деления десятичной дроби на натуральное число.

Например, ;     .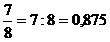

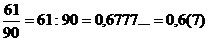b)Чтобы обратить конечную десятичную дробь в обыкновенную, достаточно в числителе дроби записать число, стоящее после запятой, а в знаменателе – единицу с нулями, причем нулей должно быть столько, сколько цифр справа от запятой.
Например, .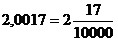

  

 c) Чтобы обратить бесконечную периодическую десятичную дробь в обыкновенную, надо из числа, стоящего до второго периода, вычесть число, стоящее до первого периода, и записать эту разность числителем, а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, и после девяток дописать столько нулей, сколько цифр между запятой и первым периодом.

Например, ; .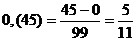

 

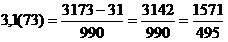Дидактический материал.

Найдите значение выражения:
1)     ;       
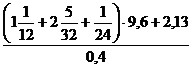2) ;

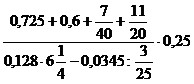3);

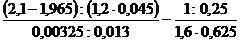4) ;

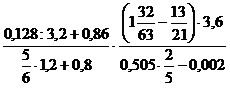5) ;       

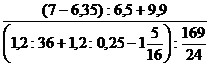6) ;

 

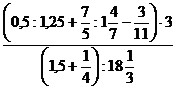7)

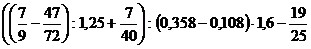
8) ;        

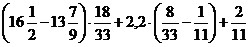9) ;

                                                      
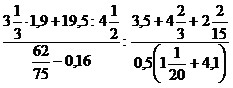10) ;
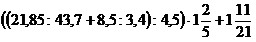11) ;

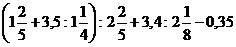12) ;

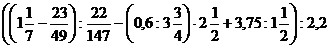13) ;

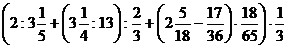14) ;

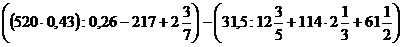15) ;

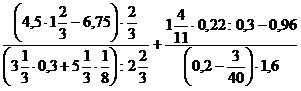16) ;        

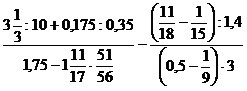17) ;

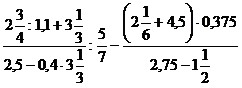18);   

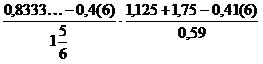19) ;

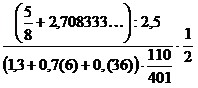20) .

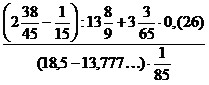Найти Х из пропорции:

21) ;

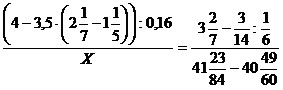22) ;

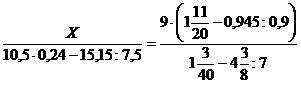23) ;
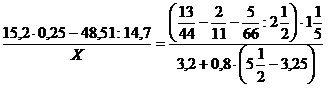24) .

 

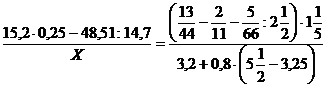Ответы: 1) 84,075; 2) 1; 3) 6; 4) 8; 5) 20; 6) 32; 7) 1; 8) 2; 9) 4; 10) 2; 11)3; 12) 3; 13) 0,5; 14) 3; 15) 1; 16) 3; 17) 5; 18) 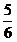; 19) 1; 20) 9; 21) 1; 

22) 5; 23) 25; 24) 5.