|
Тема №1.
Арифметические
вычисления. Проценты.
1.1 Обыкновенные
дроби. Действия над
обыкновенными
дробя.
1º.
Натуральные числа – это числа,
употребляемые при счете. Множество всех натуральных чисел обозначают N, т.е. N={1, 2, 3,
…}.
Дробью
называется число, состоящее из нескольких долей единицы.
Обыкновенной
дробью называется число вида 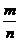 , где
натуральное число , где
натуральное число
n показывает,
на сколько равных частей разделена единица, а натуральное число m показывает,
сколько таких равных частей взято. Числа m
и n называют соответственно числителем и
знаменателем дроби.
Если числитель
меньше знаменателя,
то обыкновенная дробь называется правильной;
если числитель равен знаменателю или больше него, то дробь называется неправильной.
Число, состоящее из целой
и дробной частей, называется
смешанным
числом.
Например,
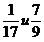 - правильные обыкновенные
дроби, - правильные обыкновенные
дроби,
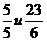 - неправильные
обыкновенные дроби, - неправильные
обыкновенные дроби,
1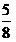 -смешанное число. -смешанное число.
2º. При выполнении
действий над обыкновенными
дробями следует помнить следующие правила:
1) Основное свойство дроби.
Если числитель и знаменатель дроби умножить или разделить на одно и то
же
натуральное число, то получится дробь, равная данной.
Например, а) 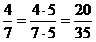 ;
б) ;
б) 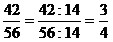 . .
Деление
числителя и знаменателя дроби на их общий делитель, отличный от
единицы, называется сокращением
дроби.
2)
Чтобы смешанное число представить в виде неправильной дроби, нужно
умножить его целую часть на знаменатель дробной части и к полученному
произведению прибавить числитель дробной части, записать полученную
сумму
числителем дроби, а знаменатель оставить прежним.
Аналогично любое
натуральное число можно записать в виде неправильной
дроби с любым знаменателем.
Например, а) 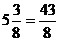 ,
так как ,
так как 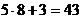 ;
б) ;
б) 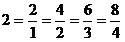
и
т.д.
3)
Чтобы неправильную дробь записать в виде смешанного числа (т.е. из
неправильной дроби выделить целую часть), нужно числитель разделить на
знаменатель, частное от деления взять в качестве целой части, остаток - в качестве числителя,
знаменатель оставить
прежним.
Например, а) 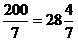 ,
так как 200 : 7 = 28 (ост. 4); ,
так как 200 : 7 = 28 (ост. 4);
б) 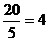 ,
так как 20 : 5 = 4 (ост. 0). ,
так как 20 : 5 = 4 (ост. 0).
4) Чтобы привести дроби к наименьшему
общему знаменателю, надо найти
наименьшее общее кратное (НОК) знаменателей этих дробей (оно и будет их
наименьшим общим знаменателем), разделить наименьший общий знаменатель
на
знаменатели данных дробей (т.е. найти дополнительные множители для
дробей),
умножить числитель и знаменатель каждой дроби на ее дополнительный
множитель.
Например,
приведем дроби 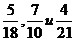 к
наименьшему общему знаменателю: к
наименьшему общему знаменателю:
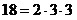 , , 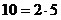 , , 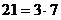 ; ;
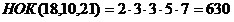 ; ;
630
:
18 = 35, 630 : 10 =
63, 630 : 21 = 30.
Значит, 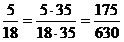 ; ; 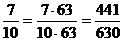 ; ; 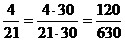 . .
5) Правила
арифметических действий над
обыкновенными дробями:
a) Сложение и
вычитание дробей с
одинаковыми знаменателями выполняется по правилу:
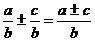 . .
b) Сложение и вычитание
дробей с разными знаменателями выполняется по правилу a), предварительно приведя дроби к
наименьшему общему знаменателю.
c) При сложении и вычитании
смешанных чисел можно обратить их в неправильные дроби, а затем
выполнить
действия по правилам a)
и b),
d) При умножении дробей
пользуются правилом:
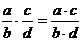 . .
e) Чтобы разделить
одну дробь на другую,
надо делимое умножить на число, обратное делителю:
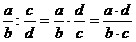 . .
f) При
умножении и делении смешанных чисел, их предварительно переводят в
неправильные
дроби, а затем пользуются правилами d) и e).
3º.
При решении примеров на все действия с дробями следует помнить, что
сначала выполняются действия в скобках. Как в скобках, так и вне их
сначала
выполняют умножение и деление, а затем сложение и вычитание.
Рассмотрим
выполнение вышеизложенных правил на примере.
Пример 1.
Вычислить: 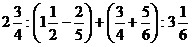 . .
1) 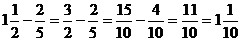 ; ;
2) 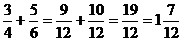 ; ;
3) 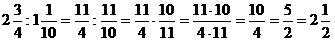 ; ;
4) 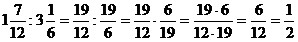 ; ;
5) 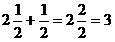 .
Ответ:
3. .
Ответ:
3.
Дидактический
материал.
Найдите
значение выражения:
1) 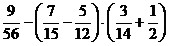 ;
2) ;
2) 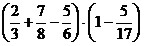 ; ;
3) 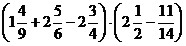 ;
4) ;
4) 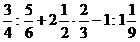 ; ;
5) 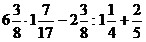 ;
6) ;
6) 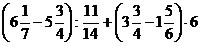 ; ;
7) 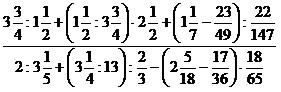 ; ;
8) 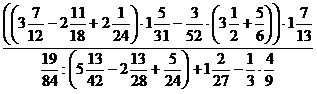 . .
Ответы: 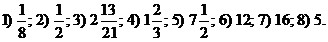
|
