2.1. Краткие теоретические положения

В основу системы сетевого планирования и управления (СПУ) положена модель, описывающая объект управления в виде сетевого графика. Благодаря этому система и получила свое название - система сетевого планирования и управления.В основу системы сетевого планирования и управления (СПУ) положена модель, описывающая объект управления в виде сетевого графика. Благодаря этому система и получила свое название - система сетевого планирования и управления.

Сетевой график имеет ряд преимуществ, в частности: на нем ясно просматриваются взаимосвязи между работами; в график легко вводятся ранее не предусмотренные работы; на графике может быть легко выявлена технологическая последовательность работ, которая определяет конечные сроки всей разработки - критический путь; по сетевому графику можно определять резервы времени работ, не лежащих на критическом пути, что позволяет наиболее рационально перераспределять наличные людские, материальные и финансовые ресурсы; этот график дает возможность оптимизировать план предстоящих работ.

Сетевой график - графическое изображение комплекса работ, отображающее взаимосвязь между событиями.

Наиболее распространенный способ изображения плана работ - это сетевой график в терминах работ и событий.

Термин "работа" используется в сетевом графике в широком смысле слова и имеет следующие значения:

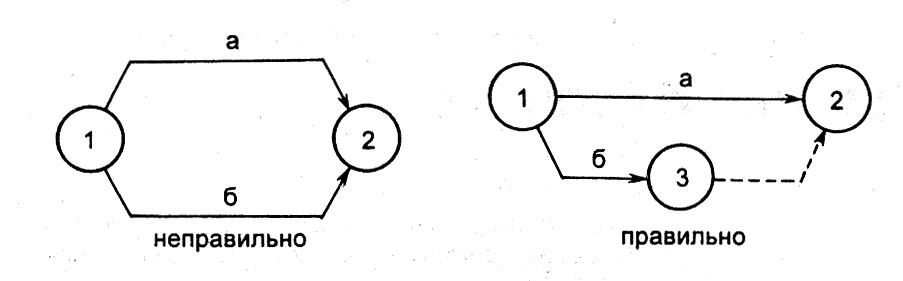
действительная работа - производственный процесс, требующий затрат времени и ресурсов (например, проектирование рабочих чертежей, изготовление деталей и т.д.);
ожидание - процесс, требующий затрат времени, но не требующий затрат ресурсов (процессы старения металла, охлаждения деталей после термообработки и т.д.);
зависимость (фиктивная работа) - условный элемент, который вводится для отражения взаимосвязи между работами (указывает что данные, полученные при свершении предшествующего события, необходимы для свершения последующего события). Зависимость не требует ни затрат времени, ни ресурсов.

Действительная работа и ожидание изображаются в сети сплошными стрелками, а зависимость - пунктирными.

Термин "событие" обозначает факт свершения одной или нескольких работ, без чего невозможно начало последующих. События изображаются на графике кружками или другими геометрическими фигурами. Событие в отличие от работы не является процессом, оно не имеет длительности, так как совершается мгновенно и не сопровождается затратами времени и ресурсов.

При построении сетевых графиков необходимо соблюдать несколько весьма несложных логических правил:

график должен быть простым, без пересечений;
стрелки (работы) должны быть направлены слева направо;
между двумя событиями может быть изображена только одна работа

для параллельно выполняемых работ вводятся дополнительное событие и зависимость

в сетевом графике не должно быть тупиков, т.е. событий, из которых не выходит ни одной работы (за исключением завершающих событий) и хвостов, т.е. событий в которые не входит ни одна работа (за исключением исходных событий), например событие 4 является тупиковым, а в событие 2 не входит ни одна работа (хвост).

в сетевом графике не должно быть замкнутых контуров (на рис. работы 1-2, 2-3, 3-1 образуют замкнутый контур)

в сетевом графике не должно быть событий, обозначенных одинаковыми кодами (на рис. одинаково закодированы два события)

сетевой график должен кодироваться так, чтобы стрелка (работа) выходила из события, закодированного меньшим числовым значением, и входила в событие с большим числовым значением.

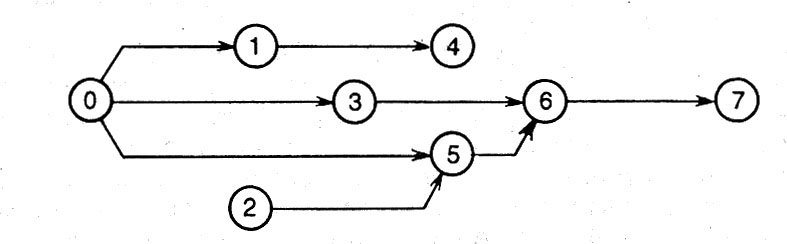
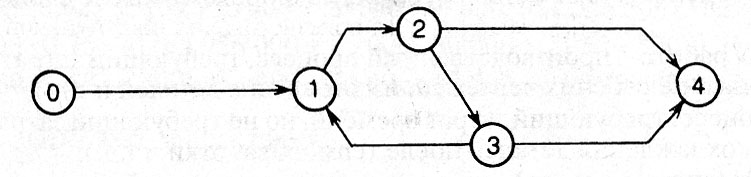
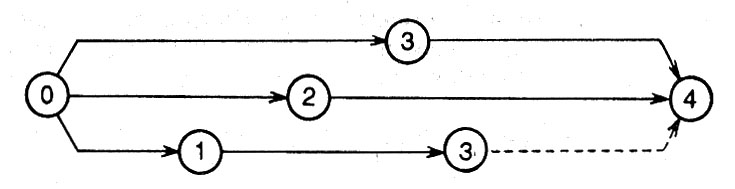
Параметры сетевого графика рассчитываются одним из способов: аналитическим, табличным, методом расчета на самом графике, с применением ЭВМ и др.

2.2. Построение сетевой модели комплекса работ

На первом этапе строится неупорядоченная сетевая модель, в которой могут иметь место пересечения некоторых стрелок, обозначающих работы. В несколько рядов наносятся кружки, которые обозначают события. Затем производится нанесение шифров событий, таким образом, чтобы событие, имеющее шифр на единицу больший, размещалось правее события, имеющего шифр на единицу меньший. После этого производится нанесение стрелок, обозначающих соответствующие работы. Это обеспечивается соединением стрелками событий, имеющих шифры, соответствующие шифрам работ.

На втором этапе необходимо построить упорядоченную сетевую модель. Это обеспечивается путем нанесения событий вновь, но те из них, которые связаны с пересекающимися стрелками, перемещаются по вертикали, а в случае необходимости и по горизонтали, таким образом, чтобы исключить имеющиеся пересечения стрелок. О правильности построения сетевой модели свидетельствует отсутствие, так называемых, хвостов и тупиков.

После определения на последующем этапе продолжительности работ сетевой модели их значения проставляются над соответствующими стрелками модели, которые обозначают работы.

2.3. Определение продолжительности работ

     В сетевой модели для каждой работы указывается ее продолжительности, которая представляет собой ожидаемое время выполнения соответствующей работы. Ожидаемое время выполнения отдельных работ определяется при помощи метода трех оценок времени. Ожидаемая продолжительность работы - tож, определяется по формуле:

t_ож = (t_min + 4t_нв + t_max)/6.

где: t_min – минимальная продолжительность работы, дни;
        t_нв – наиболее вероятная продолжительность работы, дни;
        t_max– максимальная продолжительность работы, дни.

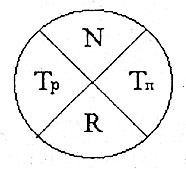
2.4. Определение путей модели и нахождение критического пути

Путь – всякая последовательность работ, соединяющая начальное событие с конечным.

Продолжительность пути t(L) определяется как сумма длительности работ, лежащих на этом пути (составляющих этот путь).

Критический путь - это полный путь модели, имеющий максимальную продолжительность. Длина критического пути Т_кр является одним из важнейших параметров сетевой модели, она указывает на общее время, необходимое для выполнения всего комплекса работ. Если сроки выполнения всех работ не укладываются в директивные (задаются преподавателем), необходимо провести оптимизацию модели, которая обеспечит сокращение критического пути до необходимых значений. В виду особого значения критического пути, на сетевом графике он выделяется: либо жирными, либо двойными стрелками, либо стрелками другого цвета.

2.5. Расчет основных параметров сетевой модели.

     К основным параметрам сетевой модели относятся: сроки свершения событий, резервы времени событий, сроки начала и сроки окончания работ и резервы времени работ.

     Среди сроков свершения событий различают: ранний срок свершения события и поздний срок свершения события.

2.5.1. Порядок расчета параметров событий.

Расчету подлежат следующие параметры:
Т_р — ранний возможный срок свершения события;
Т_п — поздний допустимый срок свершения события;
R - резерв времени события.

Расчет выполняется непосредственно на модели. В этом случае событие изображается кружком диаметром 15-20 мм, разделенным на четыре сектора (рис.). Буквой N обозначен номер события.               

Рис. Порядок расположения параметров событий

Расчет выполняется по следующим правилам:

1. Осуществляется проход сетевой модели от исходного события к завершающему и последовательно определяются ранние сроки свершения событий по формуле:

Т_рj=max(T_pi+t_ij),

где t_ij— ожидаемое время выполнения работы ij.

При этом ранний срок свершения исходного (начального) события принимается равным нулю: Т_po =0.

2. Поздний срок свершения завершающего события принимается равным полученному значению его раннего срока свершения:

Т_пз =Т_рз

Этот срок определяет длину критического пути сетевой модели (Т_кр).

3. Осуществляется проход сетевой модели от завершающего события к исходному и последовательно определяются поздние сроки свершения событий по формуле:

Т_пi=min(T_пj-t_ij)

Необходимо обратить внимание на то, что полученное в результате расчета значение позднего срока свершения исходного события должно быть равно нулю:

Т_по=Т_ро=0

4. Рассчитываются резервы времени всех событий сетевой модели по формуле:

R_i=T_пi-Т_рi

5. Выделяется на сетевой модели критический путь, как непрерывная последовательность работ от исходного события до завершающего с нулевыми резервами времени событий.

2.5.2. Порядок расчета параметров работ.

Основными параметрами работ являются:
t_рн — раннее начало работы;
t_ро — раннее окончание работы;
t_пн —позднее начало работы;
t_по— позднее окончание работы;
R_п — полный резерв времени работы;
R_с— свободный резерв времени работы

Полный резерв времени работы – это время, на которое можно увеличить при оптимизации модели продолжительность данной работы, не повлияв при этом на срок свершения завершающего события.

Свободный резерв времени работы – это время, на которое можно увеличить продолжительность данной работы, не повлияв при этом на сроки свершения как завершающего так  всех последующих за работой событий модели, следовательно, пересчета параметров не потребуется.

Расчет параметров выполняется по следующим правилам:

1. Раннее начало (t_рнij) работ, выходящих из исходного события, приравнивается к нулю. Для всех последующих работ их раннее начало приравнивается к раннему сроку свершения начального события данной работы Т_рi:

t_рнij = Т_рi,

где Т_рi-ранний срок свершения начального события данной работы

2. Раннее окончание работы tpoij определяется по формуле:

t_poij = Т_рi + t_ij

3. Поздний срок начала работы tпнij определяется по формуле:

t_пнij = Т_пj-t_ij

4. Позднее окончание работы приравнивается к позднему сроку свершения завершающего события:

t_поij = Т_пj,

где Т_пj - поздний срок свершения завершающего события

5. Полный резерв времени работы определяется по формуле

R_пij = Т_пj-Т_рi - t_ij

Работы, имеющие R_пij = 0, лежат на критическом пути сетевой модели.

6. Свободный резерв времени работы определяется по формуле:

R_сij= Т_рj–Т_рi- t_ij

2.6. Оптимизация сетевой модели комплекса работ.

Оптимизация, как правило, производится по времени. Основными параметрами, которые используются при оптимизации, являются резервы времени работ. Необходимо использовать свободный резерв времени работы, так как при этом сроки свершения всех последующих событий, и в том числе завершающего события, не изменятся и, следовательно, не потребуется пересчет параметров модели.

Суть оптимизации заключается в том, что продолжительность работ, располагающих резервами времени, может быть увеличена в пределах их резерва времени. Это означает, что часть ресурсов (трудовых, материально-технических и т.п.), связанных с выполнением соответствующих работ, может быть высвобождена и перераспределена на выполнение работ критического пути, где используются аналогичные ресурсы, что позволит сократить продолжительность этих работ и длину критического пути.

Сократить продолжительность критического пути можно перераспределением ресурсов между работами сетевой модели, когда часть ресурсов (рабочая сила) снимается с работ, не принадлежащих критическому пути и имеющих большие резервы времени, и преводится на работы критического пути, сокращая его продолжительность.

Для определения возможного количества высвобождаемых ресурсов по отдельным работам, кроме резервов времени, необходима информация о трудоемкости соответствующих работ и количестве людей (оборудования), связанных с их выполнением (см. таблицу исходных данных).

Количество работников Р, необходимое для выполнения работы, определяется по формуле:

Р = Т_р/t_ож,

где: Т_р - трудоемкость работы, чел.-дни (или чел.-час.);
     t_ож - ожидаемая продолжительность работы

По приведенной формуле определяется новая продолжительность работы в случае увеличения или уменьшения количества выполняющих ее работников. Также можно определить требуемое для выполнения работы количество исполнителей, в случае изменения ее продолжительности.

Процесс оптимизации сетевой модели может производиться многократно, пока не будет достигнута, необходимая длина критического пути. Причем, вначале оптимизация производится за счет использования внутренних ресурсов путем их перераспределения внутри модели. В случае, если это не даст необходимых результатов, возможно привлечение со стороны ранее не предусмотренных ресурсов.