|
Приведение матричной игры к задаче линейного программирования
Решение игры m x n может быть сведено к решению задачи линейного программирования.
Пусть игра m x n задана платежной матрицей 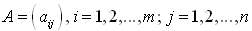 Первый игрок обладает m, второй ? n стратегиями. Необходимо определить оптимальные стратегии первого Первый игрок обладает m, второй ? n стратегиями. Необходимо определить оптимальные стратегии первого 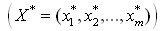 и второго и второго 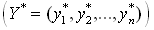 игрока, где игрока, где 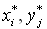 оптимальные частоты применения своих стратегий соответственно первым и вторым игроком. оптимальные частоты применения своих стратегий соответственно первым и вторым игроком.

Оптимальная стратегия X* обеспечивает первому игроку средний выигрыш, не меньший, чем цена игры V, при любой стратегии второго игрока и выигрыш, равный цене игры V, при оптимальной стратегии второго игрока.
Если первый игрок применяет смешанную стратегию X* против любой чистой стратегии второго игрока, то он получает средний выигрыш, или математическое ожидание выигрыша 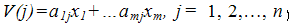 (т. е. элементы j-гo столбца платежной матрицы почленно умножаются на соответствующие вероятности стратегий первого игрока и результаты складываются). (т. е. элементы j-гo столбца платежной матрицы почленно умножаются на соответствующие вероятности стратегий первого игрока и результаты складываются).
Для оптимальной стратегии X* все средние выигрыши не меньше цены игры V, поэтому получаем систему неравенств:
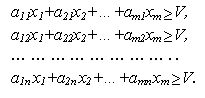 (1.4.1) (1.4.1)
Каждое из неравенств можно разделить на число V > 0. Введем новые переменные
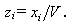 (1.4.2) (1.4.2)
Тогда система (1.4.1) примет вид:
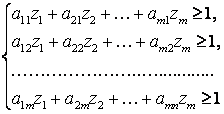 (1.4.3) (1.4.3)
Цель первого игрока — максимизировать свой гарантированный выигрыш, т. е. цену игры V. Разделив на V <> 0 равенство x1 + x2 + ... + xm = 1, получаем, что переменные zi (i=1,2,..,m) удовлетворяют условию: 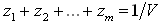 . .
Максимизация цены игры V эквивалентна минимизации величины 1/V, поэтому задача может быть сформулирована следующим образом: определить значения переменных zi >= 0 (i=1,2,..,m) так, чтобы они удовлетворяли линейным ограничениям (1.4.3) и при этом линейная функция
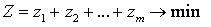 (1.4.4) (1.4.4)
обращалась в минимум. Это задача линейного программирования. Решая задачу (1.4.3) ? (1.4.4), получаем оптимальные стратегии 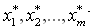
Для определения оптимальной стратегии Y* второго игрока следует учесть, что он стремится минимизировать гарантированный выигрыш первого игрока, т. е. найти max 1/V. Переменные y1,y2,...,yn удовлетворяют неравенствам
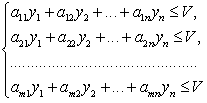 (1.4.5) (1.4.5)
которые следуют из того, что средний проигрыш второго игрока не превосходит цены игры, какую бы чистую стратегию не применял первый игрок.
Если обозначить
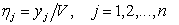 (1.4.6) (1.4.6)
то получим систему неравенств:
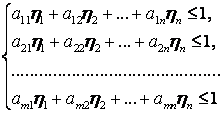 (1.4.7) (1.4.7)
Переменные 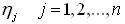 , удовлетворяют условию , удовлетворяют условию 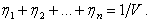
Игра свелась к следующей задаче: определить значения переменных 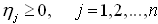 , которые удовлетворяют системе неравенств (1.4.7) и максимизируют линейную функцию , которые удовлетворяют системе неравенств (1.4.7) и максимизируют линейную функцию
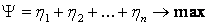 (1.4.8) (1.4.8)
Решение задачи линейного программирования (1.4.7) ? (1.4.8) определяет оптимальную стратегию Y*. При этом цена игры
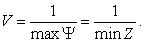 (1.4.9) (1.4.9)
Задачи линейного программирования (1.4.3) - (1.4.4) и (1.4.7) - (1.4.8) являются взаимно двойственными. Очевидно, при определении оптимальных стратегий в конкретных задачах следует выбрать ту из взаимно двойственных задач, решение которой менее трудоемко, а решение другой задачи найти с помощью теорем двойственности.
|
