|
Смешанные стратегии и теорема фон Неймана-Нэша
Ответ на вопрос, поставленный в предыдущем пункте, может быть получен благодаря применению «смешанных» стратегий.
Рассмотрим последовательность игр, в каждой из которых (k=1,..,N) игроки выбирают свои чистые стратегии и, соответственно, получают выигрыши +-aikjk. Средний выигрыш первого игрока при этом равен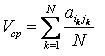
Пусть mi ? число игр, когда первый игрок выбрал свою i-тую стратегию, lj ? число игр, когда второй игрок выбрал свою j-тую стратегию, причем 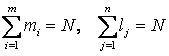
где m ? число чистых стратегий первого игрока, a n ? второго. Очевидно, что некоторые mi или lj могут быть равны нулю (если соответствующие стратегии не выбирались ни разу).
Тогда 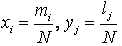 - относительные частоты выбора стратегий, - относительные частоты выбора стратегий, 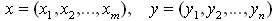 - векторы частот. - векторы частот. 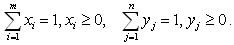
Теорема фон Неймана-Нэша
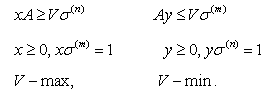
|
