|
7.5. Взаимная индуктивность в электрических цепях. Линейный трансформатор
Электрические цепи могут содержать контуры (два или более), в которых магнитный поток одного из них пронизывает другой, например, в случае двух и более параллельных линий электропередачи. Это явление называется взаимной индукцией между контурами. Если магнитный поток изменяется во времени, то в магнитосвязанных контурах наводятся ЭДС, например, ЭДС в j - том контуре при изменении тока и пропорционального ему магнитного потока в k-том определяется по формуле
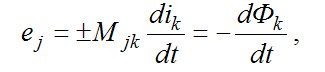
где Mjk - коэффициент взаимной индукции или взаимная индуктивность между контурами j и k , характеризует тесноту связи (коэффициент связи) между контурами. Необходимо отметить, что в электрических цепях всегда Mjk=Mkj=M . С увеличением расстояния между контурами M уменьшается. Взаимная индуктивность M , как и собственная индуктивность L , измеряется в генри (Гн).
Знаки «+» и «–» перед M означают, что выполнении расчётов цепей необходимо знать не только величину M , но и её знак, который зависит от взаимного расположения контуров; так как магнитные потоки в контуре, наводимые собственным током и током взаимного контура могут по направлению либо совпадать, либо не совпадать. В связи с этим различают согласное и встречное включение контуров (или обмоток катушек). Для определения знака, с которым добавляется потокосцепление (или поток) взаимной индукции Mik (или Mij ) к потокосцеплению самоиндукции Ljij (или Lkik ), необходимо разметить зажимы ветвей, содержащих индуктивно связанные элементы. Обычно один из зажимов первой ветви произвольно принимают за начало и наносят около него точку; вторая точка ставится у зажима второй ветви так, чтобы магнитное потокосцепление обоих индуктивных элементов увеличивалось бы вследствие взаимной индукции, когда токи ij и ik одинаково направлены относительно отмеченных зажимов своих элементов (рис.7.15).

Для установившегося синусоидального режима последнее выражение может быть записано для комплексных амплитуд 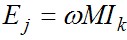 .
Если поток (потокосцепление) сцеплён только со своей обмоткой, то такой поток называется потоком рассеяния, а соответствующая ему индуктивность называется индуктивностью рассеяния. Величины, характеризующие рассеяние обозначаются индексом σ.
Трансформатор в простейшем случае представляет собой две индуктивно связанные обмотки при сильной связи между ними; для этого они должны быть надеты на общий ферромагнитный магнитопровод (сердечник). Практическое значение трансформаторов заключается, прежде всего, в возможности изменения величин напряжения. При сильной связи между обмотками почти одинаковый поток Ф пронизывает каждый из витков, поэтому ЭДС, индуктируемые в обмотках, пропорциональны числам витков w обмоток. Если к первой (первичной) обмотке с числом витков w1 приложить напряжение U1 , то напряжение U2 на зажимах второй (вторичной) обмотки с числом витков w2 можно определить по формуле .
Если поток (потокосцепление) сцеплён только со своей обмоткой, то такой поток называется потоком рассеяния, а соответствующая ему индуктивность называется индуктивностью рассеяния. Величины, характеризующие рассеяние обозначаются индексом σ.
Трансформатор в простейшем случае представляет собой две индуктивно связанные обмотки при сильной связи между ними; для этого они должны быть надеты на общий ферромагнитный магнитопровод (сердечник). Практическое значение трансформаторов заключается, прежде всего, в возможности изменения величин напряжения. При сильной связи между обмотками почти одинаковый поток Ф пронизывает каждый из витков, поэтому ЭДС, индуктируемые в обмотках, пропорциональны числам витков w обмоток. Если к первой (первичной) обмотке с числом витков w1 приложить напряжение U1 , то напряжение U2 на зажимах второй (вторичной) обмотки с числом витков w2 можно определить по формуле
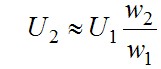 . .
Отношение вторичного напряжения к вторичному называется коэффициентом трансформации k= U2 /U1 . Если k>1 , то трансформатор называется повышающим, если k<1 - понижающим.
Трансформатор, не имеющий потерь в магнитопроводе в проводах обмоток, называется идеальным. Для идеального трансформатора коэффициент трансформации можно определить как отношение чисел витков обмоток
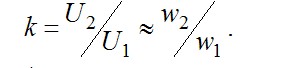
Кроме того, трансформатор изолирует первичную и вторичную обмотки в электрическом отношении, сохраняя возможность передачи энергии между обмотками.
Ферромагнитный сердечник может привести к нелинейной зависимости между первичным и вторичным напряжениями. Здесь мы ограничимся анализом работы трансформатора лишь в линейном режиме, когда все потокосцепления прямо пропорциональны токам и могут быть выражены через собственные и взаимные индуктивности, величины которых не зависят от величины тока. В таком режиме работают измерительные трансформаторы и трансформаторы в системах сигнализации, связи, радиотехнической и телевизионной аппаратуре. В близком к линейному режиму работают силовые трансформаторы в энергосистемах; нелинейность их параметров проявляется практически только в режиме холостого хода и некоторых анормальных режимах.
Основные уравнения и векторная диаграмма линейного трансформатора. Предположим, что первичная обмотка трансформатора подключена и источнику синусоидальной ЭДС . Будем также считать, что числа витков первичной и вторичной обмотки равны w1=w2 , если же w1 ≠ w2, то параметры одной обмотки должны быть приведены ко второй (приведение второго правила Кирхгофа, используя символический метод (рис.7.16, а)

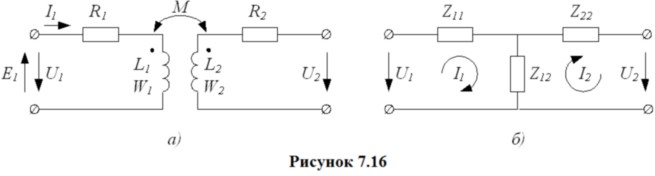
Для практических расчётов пользуются схемами замещения трансформаторов, в которых магнитная связь между обмотками заменяется электрической. Наиболее часто используется Т-образная схема замещения (рис.7.16, б). Здесь 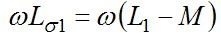 и и 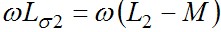 - сопротивления рассеяния первичной и вторичной обмоток соответственно, - сопротивления рассеяния первичной и вторичной обмоток соответственно,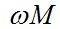 - сопротивление ветви намагничивания (в ней протекает ток намагничивания). - сопротивление ветви намагничивания (в ней протекает ток намагничивания).
Построим качественную векторную диаграмму трансформатора (рис.7.17). Построение начинают с векторов напряжения и тока вторичной цепи, соответственно, 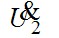 и и 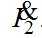 . Обычно трансформаторы в электроэнергетических установках имеют активно-индуктивную нагрузку; в этом случае вектор тока . Обычно трансформаторы в электроэнергетических установках имеют активно-индуктивную нагрузку; в этом случае вектор тока 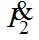 отстаёт от вектора напряжения отстаёт от вектора напряжения 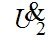 на угол на угол 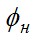 , причём , причём 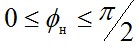 . Падение напряжения . Падение напряжения 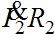 на активном сопротивлении R2 совпадает по фазе с вектором тока, падение напряжения на индуктивном сопротивлении рассеяния на активном сопротивлении R2 совпадает по фазе с вектором тока, падение напряжения на индуктивном сопротивлении рассеяния 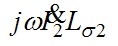 - опережает его на - опережает его на 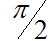 . Суммируя геометрически векторы: . Суммируя геометрически векторы: 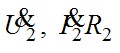 и и  получим падение напряжения на ветви намагничивания от тока намагничивания получим падение напряжения на ветви намагничивания от тока намагничивания 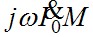 . Ток намагничивания равен геометрической разности первичного и вторичного токов . Ток намагничивания равен геометрической разности первичного и вторичного токов
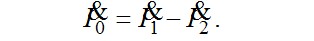
Падение напряжения на ветви намагничивания это ЭДС индуцируемая во вторичной обмотке 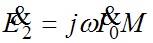 и ток намагничивания отстаёт от неё на и ток намагничивания отстаёт от неё на 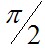 . Суммируя геометрически векторы вторичного тока . Суммируя геометрически векторы вторичного тока 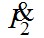 и тока намагничивания и тока намагничивания 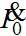 , получим вектор первичного тока , получим вектор первичного тока 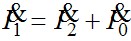 . .
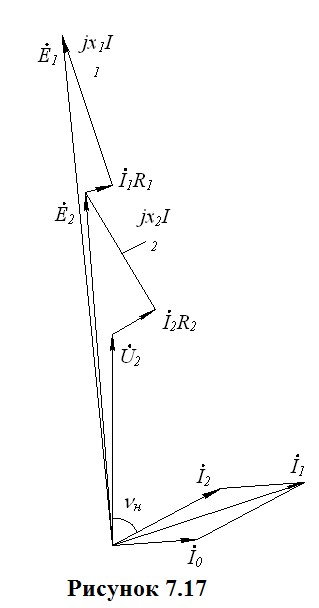
Падение напряжения от первичного тока на активном сопротивлении 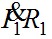 совпадает по фазе с вектором тока, на индуктивном сопротивлении рассеяния совпадает по фазе с вектором тока, на индуктивном сопротивлении рассеяния 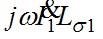 - опережает его на - опережает его на 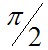 . Суммируя геометрически векторы: . Суммируя геометрически векторы: 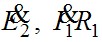 и и 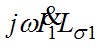 получим вектор ЭДС, приложенной к первичной обмотке получим вектор ЭДС, приложенной к первичной обмотке 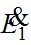 . .
|





