|

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ЦЕНТР ДИСТАНЦИОННОГО ОБУЧЕНИЯ
Кафедра «Сервис и техническая эксплуатация автотранспортных средств»
Конструкция, расчет и потребительские свойства автомобилей
ЭКСПЛУАТАЦИОННЫЕ СВОЙСТВА АВТОМОБИЛЯ
ТЕОРИЯ И РАСЧЕТ
Учебное пособие
4.2. Схема колебательной системы автомобиля
При исследовании колебаний все массы, составляющие автомобиль, делятся на две группы: массы подрессоренные и
неподрессоренные. Подрессоренными считаются массы, вес которых передается на упругие элементы подвески. У автомобилей подрессоренными массами являются
кузов и рама с укрепленными на ней механизмами; колеса в сборе с осями (мостами) относятся к неподрессоренным массам.
Реальная подвеска автомобиля может быть представлена схемой на рис. 25. Подрессоренные массы автомобиля mпзакреплены
на эластичных элементах подвески, имеющих жесткость Ср. Эластичные элементы соединены с неподрессоренными массами mн, которые через шины,
имеющие жесткость Сш, опираются на дорогу.
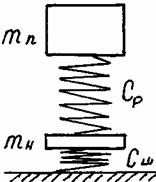
Рис.25.Схема колебательной системы подвески автомобиля с неподресоренными массами
При составлении уравнения колебательного движения подрессоренной массы в этом случае получающиеся выражения
оказываются неудобными для пользования, а с допустимой для практики точностью можно учитывать неподрессоренные массы. Это объясняется тем, что величина
неподрессоренных масс по сравнению с подрессоренной обычно очень мала, жесткость шин также значительно выше жесткости подвески (табл. 3).
Таблица 3
Суммарные жесткости подвески и шин
| Автомобиль |
Жесткость, Н/см |
| Передние колеса |
Задние колеса |
| подвеска |
шины |
подвеска |
шины |
«Москвич»
«Волга»
ЗИЛ-164
ГАЗ-51 |
340
480
2080
1770 |
3600
4400
12400
9700 |
460
530
3240
2960
|
3600
4900
20000 |
Таким образом, схема для исследования свободных колебаний автомобиля может быть принята в упрощенном виде, без учета
неподрессоренных масс mн.
Для исследования колебательного движения с упрощенной схемой можно использовать уравнения, известные для свободных
незатухающих колебаний тела, подставив в них вместо жесткости пружины С приведенную жесткость рессор и шин Спр.
Для определения приведенной жесткости подвески и шин подсчитываем суммарный прогиб такой упругой связи:
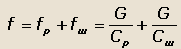
где fр и fш - прогибы рессор и шин под действием груза G.
Тогда приведенная жесткость подвески и шин будет равна:
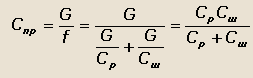 |
(31) |
Подресоренная часть автомобиля, как всякое свободное тело в пространстве обладает шестью степенями свободы и может
иметь следующие колебательные движения (рис. 26):
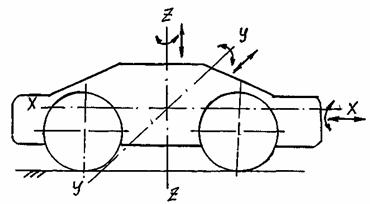
Рис.26. Схема колебательной системы автомобиля
Линейные: вдоль оси Z-Z....................подпрыгивание
вдоль оси X-X........................подергивание
вдоль оси y-y........................пошатывание
Угловые: вдоль оси Z-Z....................галопирование
вдоль оси X-X........................покачивание
вдоль оси y-y........................виляние(рыскание)
Ввиду сложности исследования системы со многими степенями свободы обычно при элементарном анализе плавности хода
автомобиля рассматривают только два вида колебаний подрессоренных масс: вертикальные линейные (вдоль оси Z-Z) и угловые продольные (относительно оси y-y).
В соответствии с этим в дальнейшем будем рассматривать колебания автомобиля как тела, имеющего две степени свободы. Кроме того, для упрощения выводов
не будем учитывать влияние неподрессоренных масс, амортизаторов и эластичности подушек сидений. Расчетная колебательная система примет вид, показанный
на рис. 27. Рассмотрение схемы показывает, что колебания автомобиля можно представить в виде колебаний отрезка АВ, проходящего через центр тяжести С
автомобиля, причем точки А и В отрезка расположены над опорами передних и задних колес.
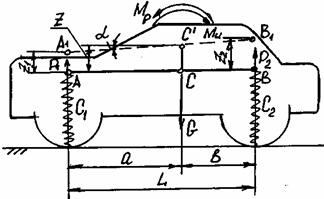
Рис.27. Расчетная схема колебательной системы автомобиля
Рассмотрим некоторое промежуточное положение отрезка АВ. Пусть отрезок из своего нейтрального положения в результате
колебаний переместился в положение А1В1.
Центр тяжести С отрезка переместился на некоторую величину Z и занял положение С', а сам отрезок повернулся на угол α.
Составим уравнение колебаний отрезка АВ.
Снизу вверх на отрезок действуют реакции эластичных элементов равные:
В точке А: P1=G1-C1Z1
В точке B: P2=G2-C2Z2
где G1 и G2 - части веса подрессоренной массы, приходящиеся на переднюю и заднюю подвески;
С1 и С2 - приведенные жесткости передней и задней подвески и шин;
Z1 и Z2 - перемещение точек А и В кузова.
В центре масс отрезка АВ действуют силы вниз:
| сила инерции |
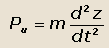 |
и вес подрессоренных масс G.
Уравнение колебательного движения будет
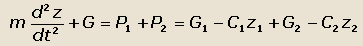
| или |
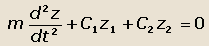 |
(32) |
Это выражение является дифференциальным уравнением вертикальных колебаний автомобиля.
Для составления дифференциальных уравнений угловых колебаний автомобиля рассмотрим моменты сил, которые его нагружают. Момент Мрсил,
создаваемых рессорами, стремящийся повернуть автомобиль относительно оси, проходящей через центр масс перпендикулярно продольной плоскости симметрии кузова,
определим по выражению:
Mp=P2b-P1a
Инерционный момент Ми, сопротивляющийся этому повороту отрезка АВ (кузова автомобиля), равен:
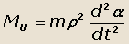
где ρ- радиус инерции подрессоренной массы автомобиля относительно оси, проходящей через центр масс перпендикулярно плоскости симметрии.
Эти моменты в каждый момент времени равны:
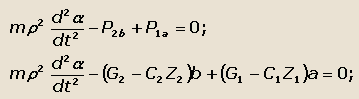
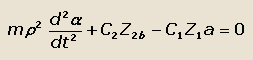 |
(33) |
Для анализа колебательных движений автомобиля важным является изучение параметров движения точек А и В. Пользуясь схемой на рис.27, определяем
величины перемещений Z1 и Z2 этих точек:
Z1=Z-atgα≈Z-aα,
Z2=Z+btgα≈Z+bα.
Дифференцируя эти уравнения дважды, получим:
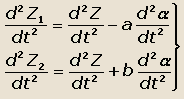 |
(34) |
Для более удобного исследования уравнений (34) величина d2Z/dt2 и d2α/dt2 заменяют параметрами,
характеризующими автомобиль. Определяя эти
величины из уравнений (31) и (32) и подставляя в выражения (34) получим:
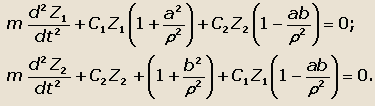
Определяя из второго уравнения величину Z2 и подставляя ее выражение в первое уравнение, получим:
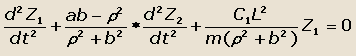 |
(35) |
И наоборот, из первого уравнения определяя величину Z1 и подставляя ее выражение во второе уравнение, получим:
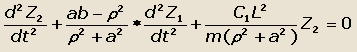 |
(36) |
По аналогии с уравнением (32) колебательного движения коэффициенты перед перемещениями Z1 и t2 представляют собой квадраты угловых частот колебаний точек А и В
автомобиля, Эти угловые частоты ω1 и ω2 называются парциальными и соответственно равны:
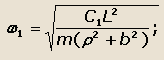 |
(37) |
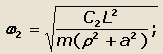 |
(38) |
Тогда
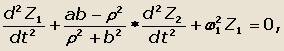 |
(39) |
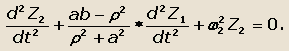 |
(40) |
Из полученных уравнений следует, что вертикальные колебания точек А и В автомобиля (см. схему на рис. 27) зависят друг от друга. При возбуждении колебаний одной
из точек возникают колебания другой точки.Очевидно, что если колебания одной точки не будут отражаться на колебаниях другой, то колебания автомобиля будут
меньше.
Анализ уравнений (39) и (40) показывает, что независимость колебаний точек А и В возможно лишь в том случае, когда в каждое уравнение войдет лишь одна переменная
(Z1 или Z2), что возможно при условии:
ab-ρ2=0; ab=ρ2
Уравнения колебаний (39) и (40) в этом случае принимают вид:
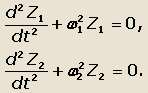
Частоты колебаний соответственно равны:
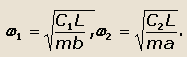
Схема колебательной системы автомобиля при условии, когда ав=ρ2представлена, на рис. 28.
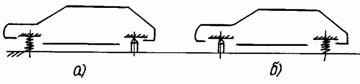
Рис.28. Схема колебательной системы автомобиля при ab=ρ2
а) — Z2=0; б) — Z1=0
На рис. 28.а показано колебание передней части автомобиля с частотой ω1 при неподвижной задней опоре. На рис.28,б показано колебание задней
части автомобиля с частотой ω2 при неподвижной передней опоре.
При ав=ρ2 колебания передней и задней частей автомобиля независимы и происходят относительно точек опоры, соответственно задних и передних колес,
а при ав≠ρ2 колебания передней части кузова зависят от колебаний задней части кузова и каждое из колебаний происходит вокруг какого-то своего центра
колебаний. Эти центры можно определить анализируя колебания кузова при возбуждении их в передней или задней части автомобиля.
Рассмотрим случай возбуждения колебаний передней части кузова (Рис. 29.а).
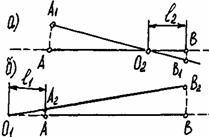
Точка А, лежащая над передней осью автомобиля, в некоторый момент времени заняла положение А1. В тот же момент времени точка В заняла положение
В1. Соединяя точки А1 и В1, получим линию, точка О2 пересечения которой с первоначальным положением отрезка АВ дает положение
заднего центра колебаний. Любые положения точек А1 и В1 кузова в процессе колебаний, взятые в один момент времени, определят тот же центр
колебаний О2.
При сообщении колебаний задней части кузова (рис. 29.б) в какой-то момент времени точка В займет положение В2 а точка А – положение А2.
Новое положение отрезка позволит тем же путем определить передний центр колебаний О1.
Результат исследования позволит найти величины l1 и l2, определяющие собой положение переднего О1 и заднего О2
центров колебаний.
Проведённый анализ показывает, что колебания кузова автомобиля складываются из двух колебаний, которые происходят вокруг двух различных центров и в общем
случае имеют разные частоты.
При конструировании автомобиля представляется возможным получить оба вида колебаний с любыми частотами. Теоретические исследования показывают, что для получения
меньших общих колебаний автомобиля необходимо, чтобы эти частоты по возможности совпадали.
| 