Введение

Начало теории графов как математической дисциплины было положено Эйлером в 1736 г. при изучении

лабиринтов и головоломок. В дальнейшем теория графов развивалась благодаря исследованиям электрических сетей и сетей дорог между населёнными пунктами, изучению моделей кристаллов, структур молекул. Англичанин Краскал с помощью графов определил условие, при котором обеспечивается минимальная длина дорог между населенными пунктами, не расположенными на одной линии.

А.М.Бутлеров разработал теорию строения молекул из атомов, используя некоторые виды графов, на которых

удобно указывать величину и характер валентных связей. Д.Кениг в 1936г. впервые объединил все схематические изображения, состоящие из совокупности точек и линий, общим термином «граф» и стал рассматривать граф как самостоятельный математический объект независимо от его конкретного содержания. Основы теории графов изложены в работе О.Оре [7]. В настоящее время практическое приложение графов развивается под влиянием теорий игр и передачи сообщений, проблем биологии. Широкое и разностороннее использование графов объясняется их наглядным геометрическим содержанием, как конфигурации из системы точек (вершин) и соединяющих их линий-звеньев. Вершины символизируют отдельные объекты или явления (атомы, города, технологические операции и т.д.), принадлежащие к цельным системам или процессам. Звенья являются мерой качественной или количественной связи между вершинами и характеризуют расстояния, силовые взаимодействия, время, валентность или другие показатели.

В машиностроении фрагменты графов находят применение при оценке размерных цепей между деталями и их

отдельными поверхностями для достижения необходимой точности [1,2,3,5]. Рассматриваемые в этих работах размерные цепи являются, по существу, частными циклами графа.

Используемые графы можно условно разделить на две группы: однородные и обобщенные. В однородных

графах все вершины равноценны по значимости. Примерами таких графов являются: система размеров на детали, сеть дорог между населенными пунктами и т.д.

В обобщенном графе каждая предыдущая вершина содержит больший объем менее конкретной информации,

чем последующая вершина. Иногда последующая вершина является результатом развития предыдущей. Примером обобщенного графа является классификация режущих аппаратов уборочных машин (рис.1).

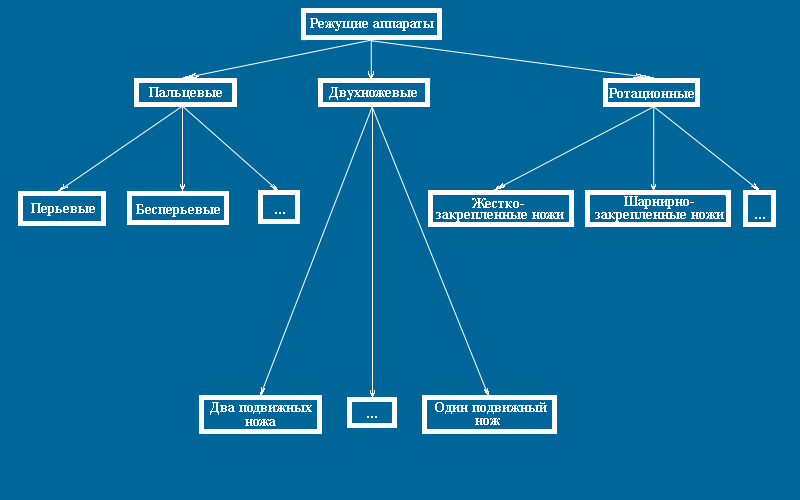
Рис.1. Классификационная схема режущих аппаратов

В обобщенном графе звено может также характеризовать степень соответствия объекта конкретному служебному назначению. На практике это соответствие

чаще оценивается качественно из-за недостатка количественной информации.

Некоторые из рассматриваемых графов ориентированы , так как их звенья являются векторами (классификационная схема, последовательность

технологического процесса и т.д.), звенья неориентированных графов являются скалярами (сеть дорог без указания маршрута передвижения, но с указанием расстояния между пунктами, химическая структура вещества и т.д.).

Однородные и обобщенные графы могут иметь нециклическую, т.е. древовидную структуру, или циклическую, т.е. замкнутую структуру.

Нециклические графы целесообразно использовать для оценки целостности объекта (процесса), структуризации и соподчинения одних вершин другим, проверочных работ. Циклические замкнутые графы позволяют выяснить размер одного из своих звеньев, например, оценить точность взаимного расположения поверхностей в детали или деталей в сборочной единице.

Для многомерной оптимизации какого-либо процесса (объекта) необходимо построить многослойный граф, установить весомость его звеньев, а затем провести

комплексный анализ [4].

Применительно к машиностроительному производству можно считать, что геометрические структуры заготовки, детали или сборочной единицы состоят из

отдельных поверхностей, которые являются вершинами графа. Звенья графа связывают эти вершины в форме линейных расстояний или углов. Эти размерные связи могут быть продольными (определяют положение плоскостей и точек в системе координат), радиальными (определяют положение поверхностей вращения) или межосевыми.

Размерные связи в готовом изделии определяются его служебным назначением, учитываются прочностными показателями, кинематикой, необходимыми

зазорами или натягами и т.д. Так как каждая поверхность конструкторской структуры координируется от одной базы, то такой граф имеет древовидный характер без замкнутых циклов.

При разработке техпроцесса изготовления детали геометрическая структура состоит из поверхностей заготовки, готовой детали и промежуточных поверхностей,

отличающихся величиной припуска [6]. Такой многослойный граф не имеет замкнутых циклов.

Графы, описывающие конструкторские и технологические структуры одного изделия, могут быть связаны общими поверхностями.

В технологическом графе звенья должны быть ориентированы, это обеспечивает последовательность операций. Так как геометрические структуры могут быть

пространственными, то для их описания необходимо построение графов в трех координатных плоскостях. В таких графах звенья являются связанными и коллинеарными векторами. Связанные они потому, что закреплены в определенной точке пространства к вершине, коллинеарные они потому, что выбираются параллельными одной из координатных осей.

 

На главную