8. ОБОСНОВАНИЕ СТРУКТУРНЫХ РЕШЕНИЙ МАШИН НА ОСНОВЕ ПАРАМЕТРИЧЕСКОГО ПРОГНОЗА
При большом разнообразии технологий и обрабатываемых материалов и требований к технологическому процессу, выбор эффективных структур средств механизации является сложной задачей. Объясняется это тем, что проектируемые и существующие схемы машин в одних условиях обеспечивают минимальные затраты, а в других оказываются неэффективными.
Специфика обоснования структурных решений машин на ранних стадиях проектирования заключается в необходимости рассматривать не отдельные операции, выполняемые одной машиной, а законченную часть производственного процесса с вариантами средств его механизации.
Варианты технологии отличаются друг от друга степенью концентрации обработки продукта одной машиной или аппаратом. Степень обработки определяют операции, на которые расчленяется процесс, с распределением переходов между машинами, входящими в технологическую линию. Этим однозначно определяются их технологические схемы.
Перед исследователем возникает задача выбора технологической схемы машины. В неопределенных условиях (не повторяющихся из года в год даже на одном и том же предприятии), например, в следствии изменения хозяйственных, погодных условий, задача еще больше усложняется.
Выбор технологической схемы обычно производится на основании опыта и интуиции конструктора, который пользуется при этом упрощенными и не всегда объективными методами. Практика же рационального хозяйствования выдвигает необходимость применения научно-обоснованных методов, позволяющих прогнозировать оптимальные варианты схем, не делая лишних проб и ошибок.
8.1. Методика прогнозирования и исходные данные
Каждая машина рассматривается как составная часть технологического комплекса. Такой подход целесообразен на ранних стадиях проектирования машин, так как позволяет обосновать технологические схемы машин, входящих в технологический комплекс и структуру их парка, рассчитать потребность в них при минимизации суммарных затрат. Задача формулируется следующим образом. Для объемов работ с определенными условиями эксплуатации выявить такие варианты концентрации операций, которые для заданного технологического направления переработки сырья с присущим ему распределением условий, обеспечат минимальные значения принятого критерия.
В качестве исходной информации используются следующие данные: - Удельные приведенные затраты на обработку сырья ZLKQ (Vα) вида К в условиях q (характеризующих процесс переработки) для рассматриваемых вариантов концентрации обработки α, в зависимости от объема работ Vα; - Объем работ заданного технологического направления переработки конкретного вида сырья V; - Вероятность Рк обработки вида сырья К; - Вероятность Рq работы в условиях q.
8.2. Математическая постановка задачи
Задача сводится к минимизации функции цели:
![]() (8.1)
(8.1)
при условиях
![]() ;
;![]() (8.2)
(8.2)
где Затраты на обработку Решение исходной задачи (8.1) - (8.2), считая известным способ подсчета затрат Полагая и считая, что не зависит от объема работ применения варианта Vα получаем задачу Поскольку ограничения по k и q друг от друга не зависят, то задача (8.3) распадается на K ∙ Q задач «о ранце» с очевидным решением Если Решением задачи (8.4) будет: 1, если α = α* ; 0, если α ≠ α* ; k = 1, 2, …, K ; q = 1, 2, …, Q. ( 8.5) Vkq, если α = α* 0, если α ≠ α* ; k= 1,2, ,k,q,=1,2, ,Q ( 8.6 ) Однако, приближение рассматриваемой модели к реальным условиям требует учета зависимости коэффициентов затрат от решения, как это было показано выше, ибо в зависимости от того, какие варианты концентрации оказались отобранными (выгодными), меняется объем производства тех или иных машин и соответственно меняются различные слагаемые коэффициентов затрат. Возникает необходимость рассмотрения нелинейной задачи: где В рассматриваемых выше моделях предполагалось, что различные варианты концентрации операций α и соответствующие им варианты конкретных конструкций j-ой машины ( Коэффициенты затрат имеют такую структуру (учитывая случайность мы ограничимся линейной зависимостью L (x)): где 8.3. Определение оптимальных концентраций операций При проектировании машины параметры неизвестны, определить наиболее выгодные концентрации невозможно, ибо неясно, как одновременно выбирать вариант концентрации операций и вариант конструкции j-ой машины. Однако, можно предложить следующую схему предварительного определения “приближенно-оптимальных” концентраций операций α, по которым затем производится конструирование машин. Будем рассматривать вектор параметров Пусть известна плотность вероятности Если теперь решить задачу (8.1-8.2) для вектора Z, т.е. с коэффициентами Zαkq , то полученное решение отвечает значению целевой функции и p(L≥L) ≥ 1-γ , так как с увеличением В результате по x можно найти варианты концентраций α, принимая которые в качестве исходных и оптимизируя конструкцию машины, мы получим (с вероятностью не менее (1-γ)) затраты меньшие, чем при любых других вариантах концентраций. Процедуры отыскания Z сводится к решению следующих задач и строится следующим образом: Вектор ξ представляют в виде дискретного распределения, т.е. Если векторы после чего, положив убеждаемся, что Полученное значение в действительности может отвечать большей, чем потребуется, вероятности, т.к. если для некоторого ν0 > n’ то Это очевидно, что наши выводы окажутся еще более надежными, чем требуем. При несравнимости (покоординатной) векторов Для непрерывного распределения определить область R1 решить задачи Остальные рассуждения те же, что и для дискретного случая. Вторая из рассматриваемых задач – обычная задача линейного программирования, если границы области R1 – линейны. В силу положительности элементов матрицы В, если ограничиться областью вида Если известна не плотность, а маргинальные плотности распределения, то приходиться применять принцип равных влияний. Ввиду сложности подобного рода задач и объёмности вычислений необходимо применение ЭВМ. Блок-схема алгоритма решения данных задач приведена на рис.8.1. Рис.15. Блок-схема алгоритма решения задачи. ![]() - объем работы, выполняемый вариантом α в условиях на виде сырья
- объем работы, выполняемый вариантом α в условиях на виде сырья ![]() подсчитываются по исходным данным, а берутся для подотрасли в целом.
подсчитываются по исходным данным, а берутся для подотрасли в целом.![]() , следующее. - В связи с большими объемами V, Рk, рq требование целочисленности Dαkq может быть опущено. Задача допускает естественное упрощение, которое сводится к следующему.
, следующее. - В связи с большими объемами V, Рk, рq требование целочисленности Dαkq может быть опущено. Задача допускает естественное упрощение, которое сводится к следующему.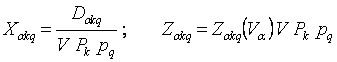
![]() (8.3)
(8.3)![]()
![]()
![]() для всех α, k, q.
для всех α, k, q.![]() (8.4)
(8.4)![]()
![]()
![]()
![]() (т.е. α* - номер варианта, отвечающий минимальным предельным затратам).
(т.е. α* - номер варианта, отвечающий минимальным предельным затратам).![]()
![]()
![]() ;
; ![]() (8.7)
(8.7)![]() ,
,![]() обычно выпуклая вверх функция и задача многоэкстремальная.
обычно выпуклая вверх функция и задача многоэкстремальная.![]() - множеству номеров машин, допускающих данную концентрацию операций) известны.
- множеству номеров машин, допускающих данную концентрацию операций) известны.![]() (8.8)
(8.8)![]() - некоторые векторы коэффициентов;
- некоторые векторы коэффициентов; ![]() - векторы параметров j-ой машины, входящей в технологический комплекс.
- векторы параметров j-ой машины, входящей в технологический комплекс.![]() как случайный, варьируемый с заданным распределением вероятностей (для фиксированной технологической схемы такое распределение, исходя из опыта проектирования машин, можно считать известным). Тогда вектор коэффициентов Z также будет случайной величиной, линейно зависящей от вектора
как случайный, варьируемый с заданным распределением вероятностей (для фиксированной технологической схемы такое распределение, исходя из опыта проектирования машин, можно считать известным). Тогда вектор коэффициентов Z также будет случайной величиной, линейно зависящей от вектора![]() (8.9)
(8.9)![]() распределения вектора
распределения вектора ![]() . Тогда по заданному доверительному уровню γ можно определить нижнюю доверительную границу Z
. Тогда по заданному доверительному уровню γ можно определить нижнюю доверительную границу Z  (8.10)
(8.10)![]() (8.11)
(8.11)![]() может только расти, поскольку ограничения от Z не зависят.
может только расти, поскольку ограничения от Z не зависят.![]() допускают координатное упорядочение
допускают координатное упорядочение ![]() , а матрица В – неотрицательна, то определяется номер
, а матрица В – неотрицательна, то определяется номер ![]()
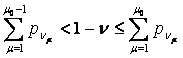 (8.12)
(8.12)![]() (8.13)
(8.13)![]() , т.е. можно принять z = z.
, т.е. можно принять z = z.![]() (8.14)
(8.14)![]()
![]() , но неотрицательности матрицы В, можно перейти к маргинальным вероятностям дискретных значений отдельных координат и произвести действия, описанные в пункте по каждой координате в отдельности.
, но неотрицательности матрицы В, можно перейти к маргинальным вероятностям дискретных значений отдельных координат и произвести действия, описанные в пункте по каждой координате в отдельности.![]() достаточно:
достаточно:![]() (8.15)
(8.15)![]() (8.16)
(8.16)![]() задача решается особенно просто:
задача решается особенно просто:![]() (8.17)
(8.17)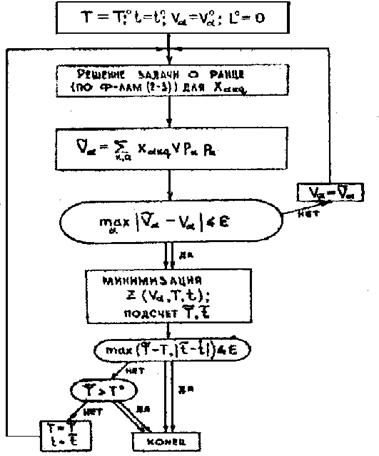
На главную