|
2. Построение математической модели
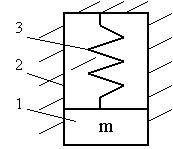
Инерционные методы измерения параметров линейного движения твердого тела основаны на измерении силы инерции F ( t ) , которая пропорциональна массе m и ускорению тела a [1] . На рис. 1 приведена схема механической системы прибора, состоящей из тела 1 массой m , движущегося поступательно по направляющим 2 и пружины 3.
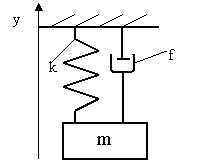
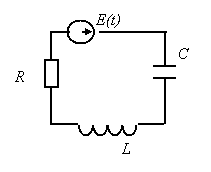
a) б) Рис. 1. Кинематическая (а) и эквивалентная (б) схема механической системы прибора Аналогами механической колебательной системы являются дуальные электрические цепи, состоящие из идеальных источников силы тока I ( t ) , напряжения U ( t ) , сопротивления R , емкости C и индуктивности L (рис. 2) [2].
Рис. 2 Электрические аналоги механической системы В соответствии со вторым законом Ньютона получим дифференциальное уравнение [1]:
где f - коэффициент вязкого трения, H * c / m ; k - жесткость пружины, H / m ; y(t) - перемещение тела, м; F(T) - внешняя сила, приложенная к телу, H. Коэффициент вязкого трения определяется по формуле f= m S/ d , где m - коэффициент динамической вязкости масла, Пас; S – площадь поверхности контакта, м 2 , d - толщина слоя масла, м. Жесткость цилиндрической пружины определяется по формуле
где G - модуль упругости второго рода, для сталей G =0.8*10 11 Па, i - рабочие число витков пружины i = i св +0.5, i св - число свободных витков пружины ; r - средний радиус витка пружины, м (рис. 2). Преобразуем уравнение (1), разделив каждый его член на жесткость пружины k , получим [2, 3]:
где m/k=T^2 , T – постоянная времени системы, с; f / k = 2 Полученное дифференциальное уравнение является уравнением второго порядка и для численного решения его необходимо преобразовать в системы дифференциальных уравнений первого порядка. Запишем уравнение (3) в явном виде
обозначив
В системе MATLAB [4] для решения ОДУ и их систем первого порядка используется ряд функций, которые реализуют методы Рунге-Кутта различных порядков с автоматическим выбором шага численного интегрирования. Ниже приведены тексты программ на языке MATLAB [4]. Тексты программ набираются в коде ASCII и называются m -файлами и имеют расширение < имя>. m M - файл головной программы моделирования колебательной механической системы % Программу составил доцент Литвин А.В. % Кафедра "Приборостроение" ДГТУ, май 2004 % % Введем исходные параметры колебательной механической системы % m - масса тела в [кг]; % d - диаметр проволоки пружины; % ni- число свободных витков пружины; global T dzeta; m=1e-3*input('Input mass [g] m='); d=1e-3*input('Input spring wire diameter [mm] d='); ds=1e-3*input('Input average spring diameter [mm] ds='); ni=input('Input spring coils number ni='); G=83670e6; % Модуль упругость второго рода [Па] nw=ni+0.5; % Число рабочих витков пружины k=G*d^4/(8*nw*ds^3); % Жесткость пружины mu=30e-3; % Динамический коэффициент смазки T = sqrt ( m / k ); f=0.5 dzeta=f/(2*k*T) % Коэффициент демпфирования y0=[5 0]; % Начальные условия t0=0.0; % Начальное время tfin=100*T; % Конечное время tspan=[t0 tfin];% Временной интервал моделирования [t,y]=ode23(@odefun, tspan, y0); % Решение дифференциального уравнения clf % Очистка графических окон figure(1) plot(t,y(:,1)), grid % График переходного процесса title('Transient response of the spring-mass-damper system') xlabel('Time, c.') ylabel('Mass translations amplitude, mm') pause figure(2) plot(y(:,1),y(:,2)), grid % График фазовой траектории title('Phase diagram of the spring-mass-damper system') xlabel('Mass translations, mm') ylabel('Velosity of mass translations') pause res(1)=T;, res(2)=dzeta;, res(3)=f; disp(' T dzeta f'); % Вывод результатов моделирования disp(res); dzt=input('Input needed damping ratio='); dzeta=dzt; % Решение дифференциального уравнения [ t 1, y 1]= ode 23(@ odefun , tspan , y 0); figure(3) plot(t1,y1(:,1)),grid; title('Transient response of the spring-mass-damper system') xlabel('Time, c.') ylabel('Vass translations amplitude, mm') pause figure(4) plot(y1(:,1),y1(:,2)), grid; title('Phase diagram of the spring-mass-damper system') xlabel('Mass translations, mm') ylabel('Velosity of mass translations') k 1= f ^2/(4* m * dzt ^2); % диаметр проволоки пружины d1=(sqrt(sqrt(8*ni*ds^3*k1/G)))*1e3; disp('Spring wire diameter (d1), mm'),; disp(d1);
M - файл ( odefun . m ) функции пользователя, описывающей систему ОДУ function ypr=odefun(t,y); global T dzeta % Система ОДУ ypr=[y(2); ((1e-3/T^2)-(y(2).*(2*dzeta/T))-(y(1)./T^2))];3. Амплитудно-частотная и фазовая характеристикиРазделив каждый член уравнения (1) на массу m , получим следующие дифференциальное уравнение
где Из уравнения (6), представленного в операторном виде, подставляя а) чувствительность механической системы к ускорению a
где б) чувствительность механической системы к скорости v
в) чувствительность механической системы к перемещению массы y
M - файл программы расчета АЧХ и ФЧХ механической колебательной системы инерционного прибора. % Анализ АЧХ и ФЧХ механической системы % Анализ чувствительности системы к ускорению % Программу составил доцент Литвин А.В. % кафедра "Приборостроение" ДГТУ май 2004 % % Введем исходные параметры % колебательной механической системы % m - масса тела в [г]; % d - диаметр проволоки пружины; % ni- число свободных витков пружины; m=1e-3*input('Input mass [g] m='); d=1e-3*input('Input spring wire diameter [mm] d='); ds=1e-3*input('Input average spring diameter [mm] ds='); ni=input('Input spring coils number ni='); G=83670e6; % Модуль упругость второго рода [Па] nw=ni+0.5; % Число рабочих витков пружины k=G*d^4/(8*nw*ds^3); % Жесткость пружины omega 0= sqrt ( k / m ); % Диапазон отношений частоты действующей силы % к частоте собственных колебаний eta =0:0.01:4; etf1=0:0.01:0.99; etf2=1.01:0.01:4; eta=eta'; etf1=etf1'; etf2=etf2'; etf12=etf1.^2; etf22=etf2.^2; eta 2= eta .^2; % Диапазон коэффициентов демпфирования dzeta=[0.125 0.25 0.6]; dzeta2=dzeta.^2; % Вычисление матрицы чувствительности (АЧХ) % к ускорению % и матрицу ФЧХ Sna =[]; Fna =[]; for i=1:3 Sna(:,i)=1./((1-eta2).^2+eta2.*dzeta2(i)*4).^0.5; end for i=1:3 Fna1(:,i)=-atan((etf1.*dzeta(i).*2)./(1-etf12)); Fna2(:,i)=-atan((etf2.*dzeta(i).*2)./(1-etf22)); end Fna2=Fna2-pi; Fna=[Fna1;Fna2]; etf=[etf1;etf2]; Fnaan=(Fna.*180)./pi; % Графики зависимости чувствительности Sa(eta) % к ускорению от eta=omega/omega0 figure(1) plot(eta,Sna), grid title('Amplitude-ratio vs. Frequency ratio eta') xlabel('Frequency ratio eta=omega/omega0') ylabel('Relative acceleration sensitivity') pause figure(2) plot(etf, Fna), grid title('Phase angle vs. Frequency ratio eta') xlabel('Frequency ratio eta=omega/omega0') ylabel('Phase angle, radian') pause figure(3) plot(etf, Fnaan), grid title('Phase angle vs. Frequency ratio eta') xlabel('Frequency ratio eta=omega/omega0') ylabel('Phase angle, degree') pause
|
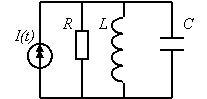
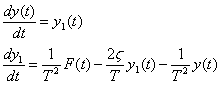 (5)
(5) 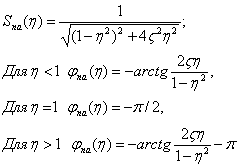 (7)
(7) 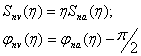 (8)
(8) 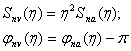 (9)
(9)