2.ОСНОВЫ КОМПЬЮТЕРНОЙ ГРАФИКИ В САПР |
|||||
| План.
2.1. Геометрические модели и синтез форм деталей Геометрической моделью объекта является его описание, содержащее сведения, однозначно определяющие его геометрическую форму. Описание формы объекта можно представить уравнениями линий и поверхностей, алгебрологическими соотношениями, списками, таблицами, графами, программами на графических языках. Теоретической основой синтеза геометрических форм являются аналитическая и дифференциальная геометрия, алгебра логики, теории множеств и графов. Геометрические модели применяются для описания геометрических свойств проектируемого объекта, решения геометрических задач, преобразования формы и положения объектов, ввода графической информации, оформления конструкторской документации. В зависимости от используемого математического аппарата различают следующие геометрические модели объектов: аналитические, алгебрологические, канонические, кинематические, каркасные, рецепторные и макромодели [1]. 2.2. Аналитические, алгебрологические и канонические модели Аналитические геометрические модели представляются уравнениями, описывающими контуры или поверхности деталей. Например, общее уравнение кривой второго порядка на плоскости в прямоугольной системе координат представлено следующим выражением [2]:
Инвариантами, определяющими свойства кривой второго порядка вне зависимости от ее положения на плоскости при переносе и повороте осей, являются:
Поверхности второго порядка определяются уравнениями второй степени. Общее уравнение второй степени относительно переменных x, y, z имеет вид:
Инвариантами, определяющими свойства поверхности второго порядка вне зависимости от ее положения в пространстве при параллельном переносе и повороте осей, являются:
В уравнениях (1)-(4) x, y, z – оси координат, a ij – постоянные коэффициенты. Кривые и поверхности можно задавать в полярной системе координат. На плоскости полярные и прямоугольные системы координат связаны соотношениями:
где ? - радиус-вектор; ? полярный угол. Полярная система координат в ряде случаев более удобна, чем декартова, однако имеет следующие недостатки: отсутствует простая связь между полярными системами координат с различным положением полюса; сложное аналитическое описание касательных и нормалей; для определения полярного угла ? необходимо использовать обратные тригонометрические функции. Уравнения (1, 3) определяют неявное задание геометрических объектов. Используются также явная и параметрическая формы задания геометрических объектов. Общий вид аналитической модели в явной форме, например, кривой на плоскости у=f(х) в параметрической форме х=х(t); у=у(t) . Аналитические модели служат для описания элементарных геометрических объектов (ЭГО), на основе которых могут быть получены составные геометрические объекты (рис.5).
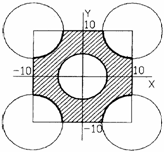
Рис. 5. Графическое изображение геометрического объекта, полученное из типовых ЭГО Алгебрологические геометрические модели обеспечивают задание плоских фигур и трехмерных тел, в которых геометрический объект описывается логической функцией условий, выражающих принадлежность точки тем или иным пространственным областям. Если, например геометрические участки G1 – G6 на плоскости x0y заданы с помощью следующих неравенств: G1: x?10, x?-10, y?10, y?-10; G2: (x-10) 2 + (y+10) 2 ?64 G3: (x+10) 2 +(y+10) 2 ?64; G4: (x+10) 2 +(y-10) 2 ?64 (6) G5: (x-10) 2 +(y-10) 2 ?64; G6: x 2 +y 2 ? 62.5, тогда геометрический объект G0 (см.рис.5, заштрихованная область) может быть записан с помощью соотношений (6) и логического выражения G1\ G2\ G3\ G4\ G5\ G6 (7) Канонические геометрические модели применяют в тех случаях, когда в геометрических объектах удается выделить параметры, которые однозначно определяют их форму. Например, для многоугольника такими параметрами могут быть число сторон многоугольника, координаты центра и радиус описанной или вписанной окружности (рис. 6).
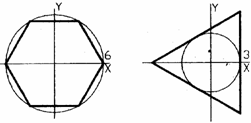
Рис. 6. Многоугольники, построенные по центру, радиусу описанной (а) и вписанной окружности (б) 2.3. Кинематические модели Кинематические геометрические модели используют параметрическую форму записи для описания плоских и пространственных линий. Поверхность может быть представлена движением жесткой или деформируемой кривой в трехмерном пространстве, тогда уравнение ?=?(V,t) (где V, t – параметры) описывает поверхность. Если один из параметров t или V зафиксировать, а другой – изменять, то можно получить плоскую параметрическую кривую трехмерной поверхности. Изме няя параметры с некоторым шагом, получим сетку параметрических кривых. Примерами простых кинематических моделей поверхностей являются поверхности вращения и линейчатые поверхности. Поверхность вращения получается в результате вращения плоской кривой вокруг оси симметрии (рис.7).
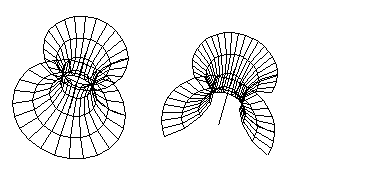
а) б) Рис. 7. Поверхности вращения, полученные поворотом дуги на 360° (а), при начальном угле поворота – 30° и конечном угле 250° (б) Линейчатой поверхностью называется поверхность, порожденная семейством прямых линий (рис.8). Примерами линейчатых поверхностей являются цилиндрические и конические поверхности. Линейчатая поверхность описывается следующим уравнением:
где ? 0 (V)- заданная точка на прямой с параметром V; ?(V)- направляющий вектор прямой.
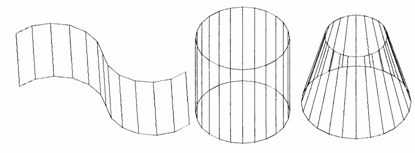
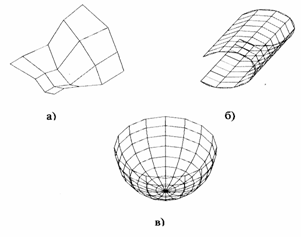
а) б) в) Рис.8. Линейчатые поверхности: поверхность сдвига (а), цилиндр (б), конус (в) 2.4. Рецепторные и каркасные модели Рецепторные геометрические модели приближенно представляют геометрический объект в плоскости (двухмерные ГО) или пространстве (трехмерные ГО) рецепторов. В области рецепторов (на плоскости или в пространстве) строится прямоугольная решетка или сеть. Каждая клетка решетки является отдельным рецептором, который может иметь два состояния – возбужденное или невозбужденное. Возбужденное состояние кодируется 1, а невозбужденное – 0. Рецептор считается возбужденным, если он включается в контур плоской или пространственной области. Таким образом, геометрический объект может быть описан двухмерной или трехмерной матрицей, состоящей из нулей или единиц. На основе рецепторных матриц можно решить большое число задач геометрического синтеза [1, 3]. Каркасные геометрические модели используют при описании поверхности в прикладной геометрии. При этом одним из основных понятий является понятие определителя поверхности. Определитель поверхности состоит из двух частей - геометрической и алгоритмической. В геометрическую часть входят геометрические объекты, а также параметры формы и положения; алгоритмическая часть задается правилами построения точек и линий поверхности при непрерывно меняющихся параметрах геометрической модели. Для воспроизведения каркасных геометрических моделей на чертежных автоматах или на ЭВМ их задают в дискретном виде (рис. 9). Дискретное множество значений параметров определяет множество линий поверхности, которое образует дискретный каркас поверхности. Непрерывный каркас поверхности из дискретного каркаса получается аппроксимацией дискретной поверхности. Непрерывные каркасы фактически являются кинематическими геометрическими моделями.
Рис. 9. Каркасные геометрические поверхности: трехмерная многоугольная сеть (а); бикубическая поверхность (б); полусфера (в) 2.5. Геометрические макромодели Геометрические макромодели являются математическим описанием типовых геометрических фрагментов. С помощью геометрических макромоделей производится изготовление конструкторско-технологичес-кой документации. Особенно широкое применение геометрические макромодели находят при подготовке рабочих чертежей. Используя типовые геометрические фрагменты, можно изображать графически шестерни, детали различных передач, винтовые соединения, подшипники и др. Контрольные вопросы
|
|||||
 (2)
(2)  ,
,  (4)
(4)