Функция правдоподобия, введённая Фишером, выглядит следующим образом:
где 
– неизвестный параметр.
В качестве оценки параметра
нужно выбрать такую величину, при которой 
достигает максимума. Поскольку
достигает максимума при том же
, что и 
, то поиск требуемого значения оценки
состоит в решении уравнения правдоподобия 
. При этом все корни 
следует отбросить, а оставить только те, которые зависят от 
.
Оценка параметра распределения является случайной величиной, которая имеет математическое ожидание и "рассеяние" вокруг него. Оценка называется эффективной, если её "рассеяние" вокруг своего математического ожидания минимально.
Справедлива следующая теорема (приводится без доказательства). Если существует
для
эффективная оценка 
, то уравнение правдоподобия имеет единственное решение. Это решение
при 
сходится к истинному значению
.
Всё это справедливо и при нескольких неизвестных параметрах. Например, для одномерного нормального закона
,
,
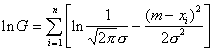отсюда 
при 
.
,
отсюда 
.
Оценка называется несмещённой, если математическое ожидание 
оценки
равно
. Оценка
является несмещённой. Действительно, поскольку 
– простой случайный выбор из генеральной совокупности, то
и 
.
Выясним, является ли 
, полученная методом максимума правдоподобия (или методом моментов),
несмещённой. Легко убедиться, что
.
Следовательно,
.
Найдём математическое ожидание этой величины:
.
Так как дисперсия
не зависит от значения 
, то выберем 
. Тогда
, 
, 
,
где 
, 
– коэффициент корреляции между 
и 
(в данном случае он равен нулю, т.к. 
и 
не зависят друг от друга).
Итак, 
. Отсюда видно, что оценка
не является несмещённой, её математическое ожидание несколько меньше,
чем 
. Для ликвидации данного смещения необходимо умножить
на 
. В результате получим несмещённую оценку
.