Метод  ближайших соседей

Здесь идея состоит в том, что вокруг распознаваемого объекта  строится ячейка объёма . При этом неизвестный объект относится к тому образу, число обучающих представителей которого в построенной ячейке оказалось большинство. Если использовать статистическую терминологию, то число объектов образа , попавших в данную ячейку, характеризует оценку усреднённой по объёму  плотности вероятности .

Для оценки усреднённых  нужно решить вопрос о соотношении между объёмом  ячейки и количеством попавших в эту ячейку объектов того или иного класса (образа). Вполне разумно считать, что чем меньше , тем более тонко будет охарактеризована . Но при этом тем меньше объектов попадёт в интересующую нас ячейку, а следовательно, тем меньше достоверность оценки . При чрезмерном увеличении  возрастает достоверность оценки , но теряются тонкости её описания из-за усреднения по слишком большому объёму, что может привести к негативным последствиям (увеличению вероятности ошибок распознавания). При небольшом объёме обучающей выборки  целесообразно брать предельно большим, но обеспечить при этом, чтобы внутри ячейки плотности  мало изменялись. Тогда их усреднение по большому объёму не очень опасно. Таким образом, вполне может случиться, что объём ячейки, уместный для одного значения , может совершенно не годиться для других случаев.

Предлагается следующий порядок действий (пока что принадлежность объекта тому или иному образу учитывать не будем).

Для того чтобы оценить  на основании обучающей выборки, содержащей  объектов, центрируем ячейку вокруг  и увеличиваем её объём до тех пор, пока она не вместит  объектов, где  есть некоторая функция от . Эти  объектов будут ближайшими соседями . Вероятность  попадания вектора  в область  определяется выражением .

Это сглаженный (усреднённый) вариант плотности распределения . Если взять выборку из  объектов (простым случайным выбором из генеральной совокупности), то  из них окажется внутри области . Вероятность попадания  из  объектов в  описывается биномиальным законом, имеющим резко выраженный максимум около среднего значения . При этом  является неплохой оценкой для .

Если теперь допустить, что  настолько мала, что  внутри неё меняется незначительно, то

,

где     – объём области ,  – точка внутри .

Тогда . Но , следовательно, .

Итак, оценкой  плотности  является величина

.                                  (*)

Без доказательства приведём утверждение, что условия

 и                         (**)

являются необходимыми и достаточными для сходимости  к  по вероятности во всех точках, где плотность  непрерывна.

Этому условию удовлетворяет, например, .

Теперь будем учитывать принадлежность объектов к тому или иному образу и попытаемся оценить апостериорные вероятности образов  

Предположим, что мы размещаем ячейку объёма  вокруг  и захватываем выборку с количеством объектов ,  из которых принадлежат образу . Тогда в соответствии с формулой  оценкой совместной вероятности  будет величина

,

а

.

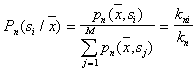Таким образом, апостериорная вероятность  оценивается как доля выборки в ячейке, относящаяся к . Чтобы свести уровень ошибки к минимуму, нужно объект с координатами  отнести к классу (образу), количество объектов обучающей выборки которого в ячейке максимально. При  такое правило является байесовским, то есть обеспечивает теоретический минимум вероятности ошибок распознавания (разумеется, при этом должны выполняться условия ).