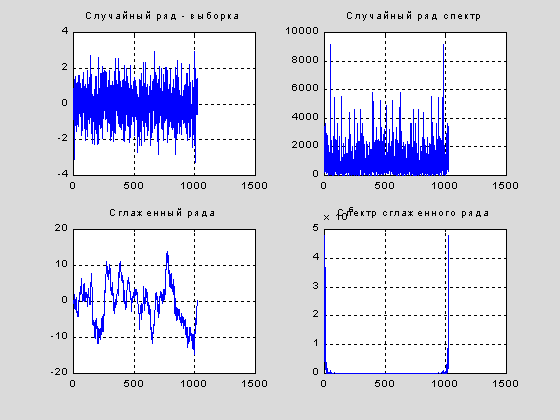
Важнейшее отличие методов анализа временных рядов от анализа случайных величин состоит в том, что считается конечным результатом исследования. Нам придется признать невозможность продолжения анализа, если будет установлено, что исследуемый ряд представляет собой выборку т.е. последовательность одинакова распределенных независимых в совокупности случайных величин. Посмотрим, что может дать в этом случае спектральный анализ. Вызовом randn создадим такую
выборку {r(n), n=1:1024} и проведем соответствующую оценку спектра. Далее проведем сглажиавние сгенерированного ряда при помощи скользящего cреднего c параметром прогноза ro=0.98: {sr(n)=r(n)+ro*sr(n-1), n=2:1024}.
| r=randn([1 1024]); |
Выборка из стандартного нормального закона |
| fr=fft(r); |
Преобразование Фурье от нее |
| dens=fr.*conj(fr); |
Мощность спектра |
| ro=0.98; b=1; a=[1 -ro]; |
Вводим параметры производящего преобразование фильтра |
| sr=filter(b,a,r); |
Здесь из r получают sr(n)=r(n)+ro*sr(n-1) |
| fsr=fft(sr); |
|
| sdens=fsr.*conj(fsr); |
subplot(2,2,1),plot(r),grid,title('Случайный ряд - выборка')
subplot(2,2,2),plot(dens),grid,title('Случайный ряд спектр')
subplot(2,2,3),plot(sr),grid,title('Cглаженный ряда')
subplot(2,2,4),plot(sdens),grid,title('Спектр сглаженного ряда')
Как видно, амплитуда сглаженного ряда заметно превышает амплитуду исходного, сами колебания преобрели выраженный систематический характер, а спектр - практически сосредоточен в низкочастотной области и не содержит заметных выбросов. С уменьшением ro, спектр начинает "растекаться", а размах колебаний сокращается. Соотношения типа X(n)=r(n)+ro*X(n-1) и Y(n)=r(n)+ro*X(n-1) (см. [10]) возникают в практике анализа временных рядов, когда делается попытка связать разновременные значения отсчетов одного и того же ряда, или различных рядов, близких по своему происхождению. Тогда и возикает мысль оценить параметр ro методом наименьших квадратов. В случае первого уравнения оценка приводит к равенству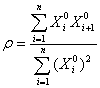 
, где 
- ряд отклонений исходного ряда от общего среднего. Величина 
называется автокорреляцией ряда с лагом 1. Если, по небольшому отрезку данных получить оценку для , то для всего ряда можно применить соотношение X1(n)=ro*X(n-1) с целью получить прогноз X(n) по X(n-1), а потом вычислить поправку r(n)=X1(n)-X(n). Если структура ряда такова, диапазон значений r(n) существенно уже, чем для X(n), то хранить и передавать значения поправок выгоднее, чем актуальные значения.
Совершенно аналогично соотношение для прогоза значений одного ряда по другому приводит к равенству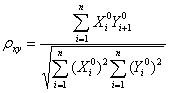 
, с аналогичными соглашениями об удалении общего среднего значения из обоих рядов. Полученная величина носит название кросс-корреляцией с лагом 1. Так возникает оценка параметров модели порождения одного временного ряда по другому с возможностью применить эту оценку к задаче упаковки данных при передаче их по линии связи или хранении. Перейдем к модельному расчету.
Идея исследуемого алгоритма состоит в следующем. Подсчитаем коэфициент корреляции двух стереоканалов. Полученный коэффициент корреляции (если он достаточно велик) позволит предсказывать значения одного ряда отсчетов по другому с достаточной точностью, т.е. ошибка потребует заметно меньше ресурса для передачи, чем все значение. Неизбежные ошибки, конечно, надо вычислить и сохранить. Польза от такого распределения ролей состоит в следующем. один ряд – ведущий – храним неизменным в разрядной сетке 16 бит, а другой – поправки – чкажем, с разрядностью 12 бит. Если вероятность клиппирования поправок при сохранении станет существенной, то после восстановления такая стереозапись заметно потеряет качество. Но, возможно, нам и повезет…
Сначала попробуем силы на связи между каналами, предполагая, что можно прогнозировать один канал по другому, и поправку сохранять:
Сначала попробуем силы на связи между каналами, предполагая, что можно прогнозировать один канал по другому, и поправку сохранять:
| N1=2000 |
Начало блока отсчетов |
| N2=5000 |
Конец блока отсчетов |
| row=N2-N1+1; |
Число строк-отсчетов |
| [x1,x2,x3]=wavread('cocer1.wav',[N1,N2]); |
Считали звуковые отсчеты в x1 (оба канала), x2 - частота дискретизации, x3 - число бит на отсчет |
| [size(x1) x2 x3] |
|
| ans = 3001 2 44100 16 |
|
| ee=corrcoef(x1) |
|
| ee = 1.0000 0.5957 0.5957 1.0000 |
ee - матрица корреляций между каналами. |
| beg=1500:3000; |
beg - индексы для графиков |
| ro=ee(1,2); |
ro - корреляция между 1-м и 2-м каналами |
| z=filter([0 ro],1,x1(:,1)); |
z - линейный прогноз с помощью коэффициента корреляции между каналами: z(t+1)=ro*x1(t,1) |
| Вычислим поправки eps, т. е. ошибку от замены отсчета в правом канале на линейный прогнозом по смежному каналу. Это соответствует формуле: eps(t+1)=x1(t+1,2)-ro*x1(t,1), а вот на графике сравнение прогноза и реального значения: eps=x1(:,2)-z(:); subplot(211),plot(beg/x2,x1(beg,1)), title('Значение в левом канале'),grid; subplot(212),plot(beg/x2,eps(beg)), title('Поправка к прогнозу значений в правом канале'),grid; Проведем вычисления коэффициентов корреляции между eps - поправкой и каналами. x1eps1=corrcoef([x1(:,1),eps]) x2eps1=corrcoef([x1(:,2),eps]) x1eps1 = 1.0000 -0.1311 -0.1311 1.0000 |
|
| x2eps1 = 1.0000 0.7173 0.7173 1.0000 |
|
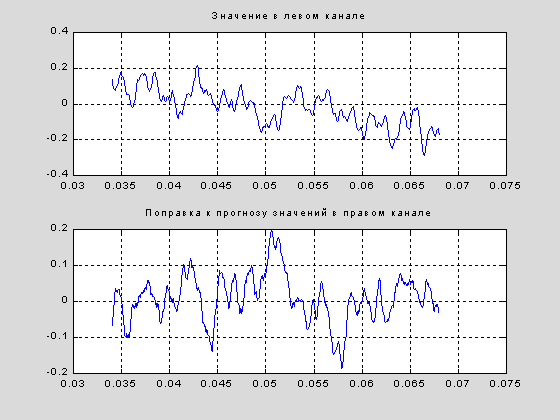
Как видим, поправка практически не зависит от значений, которые мы будем сохранять и весьма тесно связана с теми данными, которые она должна помочь восстановить.Таким образом, вычисленее поправки озачает декорреляцию, т. е. снижение избыточности хранимой информации.
Однако, давайте вычислим, сколько, все-таки поправок укладывается в отведенный для них байт, иными словами, их абсолютное значение не превосходит 1/2^3 от максимального - что даст выигрыш в четыре бита.Эту работу выполнит функция find.
help find
FIND Находит индексы ненулевых элементов
I = FIND(X) возвращает вектора X, которые соответствуют ненулевым элементам. Напимер, I = FIND(A>100), возвращаентиндексы элементов A превосходящих 100.
[I,J] = FIND(X) возвращаеи индексы строк и колон ненулевых элементов матрицы X. [I,J,V] = FIND(X) также возвращает вектор, содержащий ненулевые значенмия.
index=find(abs(eps)>1/2^3); Найдем те значения, которые вызовут переполнение (16-4)-битной разрядной сетки
prob=length(index)/length(eps)
prob =
0.0880
Ну, неплохо. А теперь вычислим характеристику, которую статистики считают оценкой качества регрессионной модели - доля выриации, которую позволяет оценить модель по сравнению с полной вариацией данных.
AllVar=var(x1) - Полная вариация
AllVar =
0.0093 0.0067
EpsVar=var(eps) - Необъясненная моделью вариация
EpsVar =
0.0045
Доля необъясненной вариации
EpsVar/AllVar(2)
ans =
0.6690
Результат настораживает. В самом деле ничего страшного. Мы и не собирались устранить все ошибки, нам было бы достаточно сохранить "достаточно высокое" качество стереозвучания. Так что последнее слова за слушателем.
Теперь попробуем связи между соседними по времени отсчетами 1-го канала, полагая, что можно прогнозировать значение отсчета в момент (t+1) по отсчету в момент t, и поправку сохранять
| x1=[x1(:,1) [0; x1(1:row-1,1)]]; |
Запишем в таблицу x1 вместо второго канала – запоздавший на один отсчет первый и проведем расчеты по предыдущему сценарию. |
| ee=corrcoef(x1) |
|
| ee = 1.0000 0.9985 0.9985 1.0000 |
ee- матрица корреляций между сдвигами |
| ro=ee(1,2); |
Корреляция между сдаигами |
| z=filter([0 ro],1,x1(:,1)); |
z - линейный прогноз с помощью коэффициента корреляции между сдвигами: z(t+1)=ro*x1(t,2) |
| eps=x1(:,2)-z(:); |
ошибка предсказания |
| beg=[N1:N2]' |
|
| subplot(2,1,1),plot(beg/x2,x1(:,1)), title('Сигнал в 1-м канале'),grid; subplot(2,1,2),plot(beg/x2, eps), title('Прогноз в в 1-м канале'),grid; |
|
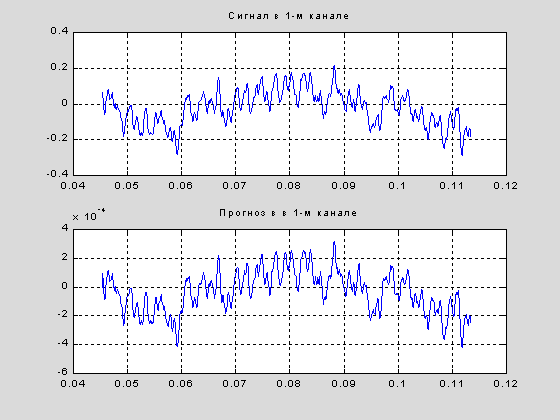
Вычисление поправки озачает декорреляцию, т. е. замену отсчета на разность между текущим значением и линейным прогнозом по уже полученному значению:
xeps=corrcoef([x1(:,1),eps])
xeps =
1.0000 0.9985
0.9985 1.0000
xeps - матрица корреляций между отсчетаим и поправкой. Ну а теперь тест на вероятность "больших" ошибок.
index=find(abs(eps)>1/2^12);
prob=length(index)/length(eps)
prob =
0.0906
Надежда на экономию в 12 бит на отсчет.