В дальнейших примерах мы познакомимся с возможностями MATLAB'а, обеспечивающими работу со звуком: со стандартными интерфейсными файлами формата RIFF (Resource Information File Format Файл Формата Информационного Ресурса), именно с Microsoft WAVE (*.wav) звуковыми файлами. Соответствующие этой цели функции общего незначения - wavread и wavwrite. (Дополнительные возможности – в Signal Toolbox – wavrecord и wavplay обеспечивают программиста потоковами возможностями ) Обращение к помощи дает:
Y=WAVREAD(FILE) читает WAVE файл, имя которого указанно в кавычках, возвращая дискретизованные данные в Y. ".wav"-расширение добавляется по умолчанию. Амплитудные значения находятся в диапазоне [-1, +1].
[Y,Fd,NBITS] =WAVREAD(FILE) возвращает скорость дискретизации (Fd) в Герцах, и число битов на отсчет (NBITS), использованных при кодировании.
[..] =WAVREAD(FILE, N) возвращает только первые N отсчетов каждого канала в файле.
[...]=WAVREAD(FILE,[N1 N2]) возвращает только отсчеты от N1 до N2 из каждого канала в файле.
SIZ=WAVREAD(FILE,'size') возвращает размер звуковых данных, содержащихся в файле на месте фактических звуковых данных, возвращая вектор SIZ = [каналы отсчеты].
[Y,FS,NBITS,OPTS]=WAVREAD(...) возвращает, структуру OPTS дополнительной информации, содержащейся в WAV файле. Содержание этой структуры отличается от файла к файлу. Типичные структурные поля включают '.fmt ' (звуковая информация формата) и '.info ' (текст, который может описывать подчиненный заголовок, авторское право, и т.д.).
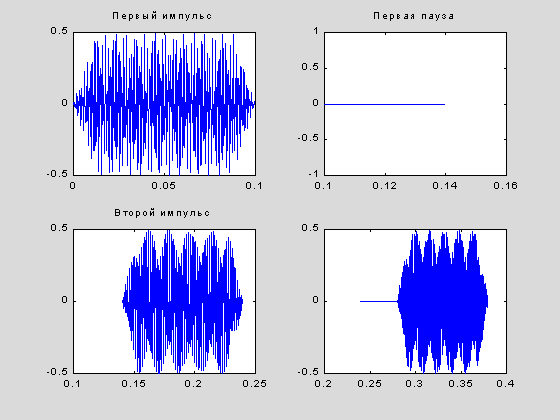
Пример обращения к данным такого рода дает следующий скрипт. В нем считываются и отображаются сигналы тонального набора телефонного номера со стандартной длительностью посылки (0.1 сек) и паузы (0.04 сек). Для примера мы используем последовательность, сответствующую набору цифр, составляющих имя файла.
*************************
[y,Fd,Nbits,opts]=wavread('126.wav');
disp(['Размер полученного массива данных: ', num2str(size(y))])
disp(['Колличество бит на отсчет: ', num2str(Nbits)])
disp(['Скорость дискретизации: ', num2str(Fd)])
time=length(y);
t1=(1:800); % Первые 0.1 сек сигнала – цифра "1"
t2=(801:1120); % Первая пауза в наборе
t3=(1121:1920); % Цифра "2"
t4=(1921:3040); % Вторая пауза и цифра "6"
grid on
subplot(2,2,1), plot((t1-1)/Fd,y(t1)),title('Первый импульс')
subplot(2,2,2), plot((t2-1)/Fd,y(t2)),title('Первая пауза')
subplot(2,2,3), plot((t3-1)/Fd,y(t3)),title('Второй импульс')
subplot(2,2,4), plot((t4-1)/Fd,y(t4)),title('Третий импульс')
***************************
Размер полученного массива данных: 3040 1
Колличество бит на отсчет: 8
Скорость дискретизации: 8000

Замечание. Переменная opts содержит служебную информацию, которая необходима для обмена данными с файлом при помощию встроенных функций fread и fwrite. Программу на вышем любимом языке можно писать, основываясь на соответствующих версиях этих функций, поскольку синтаксис обращения к ним весьма близок к языку C. Поэтому весьма поучительны тексты wavread и wavwrite с учетом тех дополнительных пояснений, которые дают обращения help wavread и т. п.
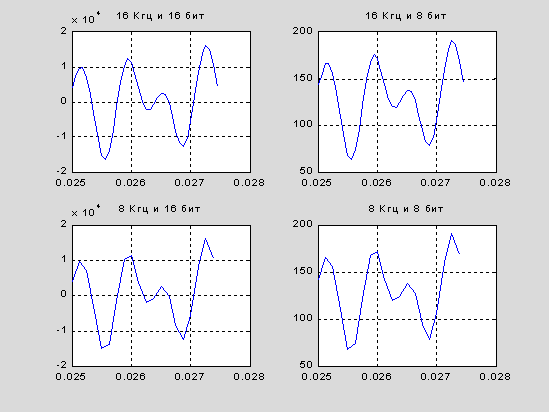
С целью прояснить роль параметров Nbits – число бит на отсчет и Fd – скорость дискретизации предпримем эксперимент – отключим с помощь знака "%" в начале строки коды строк 665 - 669:
% Нормализуем область изменения данных: min будет -1, max - +1.
if BytesPerSample==1, % если число бит на отсчет =1
dat.Data = (dat.Data-128)/128; % [-1,1)
else
dat.Data = dat.Data/32768; % [-1,1)
end
Такую измененную функцию назовем wavread1 и проведем с ней эксперимент по визуализации данных того же рода, что и раньше, именно, сигнал "9" продолженный паузой, но записанный в различной отсчетности и разрядности.
[y1,Fd1,Nbits1]=wavread1('9b16s16.wav');
[size(y1) Fd1 Nbits1]
[y2,Fd2,Nbits2]=wavread1('9b8s16.wav');
[size(y2) Fd2 Nbits2]
[y3,Fd3,Nbits3]=wavread1('9b16s8.wav');
[size(y3) Fd3 Nbits3]
[y4,Fd4,Nbits4]=wavread1('9b8s8.wav');
[size(y4) Fd4 Nbits4]
t1=(401:440);
t2=(201:220);
subplot(2,2,1), plot((t1-1)/Fd1,y1(t1)),title('16 Кгц и 16 бит'),grid
subplot(2,2,2), plot((t1-1)/Fd2,y2(t1)),title('16 Кгц и 8 бит'),grid
subplot(2,2,3), plot((t2-1)/Fd3,y3(t2)),title('8 Кгц и 16 бит'),grid
subplot(2,2,4), plot((t2-1)/Fd4,y4(t2)),title('8 Кгц и 8 бит'),grid
| Имя Файла |
Число отсчетов (строк) |
Число отсчетов (колонн) |
Частота дискретизации |
Чило бит на отсчет |
| 9b16s16 |
2240 |
1 |
16000 |
16 |
| 9b8s16 |
2240 |
1 |
16000 |
8 |
| 9b16s8 |
1120 |
1 |
8000 |
16 |
| 9b8s8 |
1120 |
1 |
8000 |
8 |
А вот какие графики получились. Обратите внимание на то, как приходилось менять параметры в переменных, обеспечивших визуализацию данных, собранных на однм и том же временнм отрезке, и как поменялся масштаб явлений по амплитуде при замене разрядности и отсчетности.
Разбор программы wavwrite начнем с перевода доступной помощи. Вот какую помощь предоставит MATLAB:
help wavwrite
WAVWRITE Записывает Microsoft WAVE (".wav") звуковой файл.
WAVWRITE(Y,FS,NBITS,WAVEFILE) записывает данные Y в Windows WAVE файл указанный именем WAVEFILE, с отсчетностью FS герц и с NBITS битов на отсчет. NBITS должно быть 8 или 16.
Стерео данные должны быть представлены как матрица из двух колон. Значения амплитуды, выходящие за пределы [-1,+1], заменяются на соответствующие крайние значения (клиппируются).
WAVWRITE(Y,FS,WAVEFILE) предполагает NBITS=16 бит.
WAVWRITE(Y,WAVEFILE) предполагает NBITS=16 бит и FS=8000 герц.
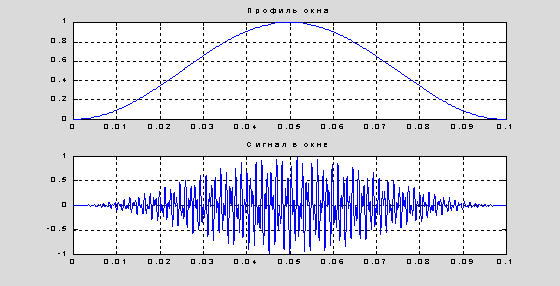
Построим wav-файл такой природы, как примененный в предыдущем пункте, предполлагая, что цифру "9" генерирует сочетание тонов 852 гц и 1477 гц. Кроме того по краям временного отрезка [0 0.4] секунд обеспечим постепенное нарастание интенсивности и ее убывание. Так делают, чтобы не создавать высокочастотных помех от "щелкания" выключателей. Вот соответствующий скрипт.
Fd=16000; nt=1:1601; t=(nt-1)/Fd;
f1=852; f2=1477;
% Окно для плавного перехода к молчанию
ycos = 0.5 * (1 - cos(2*pi*nt/(1600-1)));
y1=cos(2*pi*t*f1); y2=sin(2*pi*t*f2); y12=ycos.*(y1+y2);
Чтобы не "клиппировать", т.е. не заменять большие отклонения крайними допустимыми величинам ( в зависимости от разрядности), мы масштабируем данные в диапазон [-1.1]. Заодно посмотрим как выглядит "окно", через которое мы наблюдали за процессом.
ny=max(abs(y12))*1.01; y12=y12/ny;
subplot(211),plot(t,ycos), title('Профиль окна'),grid;
subplot(212),plot(t,y12), title('Сигнал в окне'),grid;