Описываемые далее процессы наблюдаются в приборах с дрейфом параметров в зависимости от температуры окружающей среды. Таким образом, в результате отнесения соответствующего файла наблюденных данных к одному из классов мы получаем возможность установить, при какой температуре работает прибор. Дополнительные ограничения перед разработчиками алгоритма ставит требование ограничиться возможностями аналого-цифрового преобразователя, размещенного на простой звуковой карте. Так, ограничивая скорость дискретизации величиной 8000 отсчетов в секунду и объем считываемых данных блоком отсчетов длины 64 Кбайт, мы получаем экономную схему реализации, например устройства, контролирующего температуру в бытовом помещении.
В условиях неизменной температуры ток протекающий по цепи вычисляется в соответствии с алгоритмом, приведенном ниже.
function cont=dtmp(t)
global tt pp -
% параметры, опредаляемые режимом работы прибора
% floor(a)) - округляет элементы a до
% ближайшего в направлении к (-inf) значения
t1=t-(tt+pp)*floor(t./(tt+pp));
% t1 - остаток от деления t на период (tt+pp)
cont=(t1<=tt).*(0.9+t1/tt*0.1);
% cont = 0, если доля t1 в (tt+pp) больше tt,
% иначе - cont растет от 0.9 до 1
cont=cont(:);
**********************
Здесь мы моделируем работу стенда с аналоговым представлением данных - на экране осцилографа. Такая постановка задачи означает практически недостижимую (без существенных дополнительных затрат на специальное оборудование и программное обеспечение) скорость ввода и обработки данных в ЭВМ.
|
clear all |
% Очистка памяти |
|
global tt pp sens |
% Описание глобальных переменных |
|
sens=0.4; |
% Условная характеристика термочувствительности ге % нератора, определяемая типом транзистора и режи % мом его работы |
|
Tdiap=2 |
% При температурных градациях i=0:(Tdiap-1) % исследуем спектр колебаний |
|
N=1024 |
% Длина блока, допустимого по ограничениям памяти |
|
tt=35*10^(-6); |
% Длина токовой фазы |
|
pp0=3*tt; |
% Длина бестоковой фазы при нулевой температуре |
|
fd=10^6; |
% Частота дискретизации для имитации осцилограммы |
|
fs=fd/2; |
% Частота Найквиста |
|
step=1/fd; |
% Интервал дискретизации |
|
t=0:step:step*(N-1); |
% Массив временных отсчетов для осцилограммы |
|
at=length(t); |
% Его длина |
|
yy=[]; |
% Инициализация массива значений процесса |
|
for ts=0:(Tdiap-1) |
% Начало цикла по температуре |
|
pp=(1-sens*ts)*pp0; |
% Изменяем настройку |
|
% В соответствии с ростом температуры |
|
|
% уменьшается длина бестоковой фазы |
|
|
y=dtmp(t+rand); |
% Моделируем блок данных от генератора со |
|
% случайной фазой |
|
|
yy=[yy,y]; |
% Добавляем его в массив |
|
end |
% Конец цикла по температуре |
|
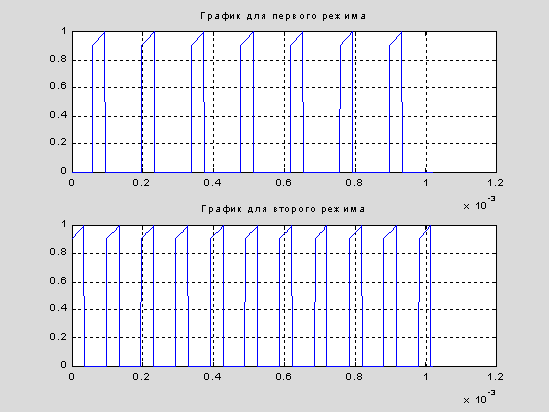
subplot(2,1,1), plot(t(1:N),yy(1:N,1)),title(' График для первого режима '), grid subplot(2,1,2), plot(t(1:N),yy(1:N,2)),title(' График для второго режима '), grid |
|
Результат вычислений и график:
Tdiap =
2
fs =
500000
pp =
1.0500e-004
pp =
6.3000e-005

Внесем в вышезаписанном скрипте следующие изменения:
|
clear all |
% Очистка памяти |
|
global tt pp sens |
% Описание глобальных переменных |
|
sens=0.02; |
|
|
Tdiap=2 |
% При температурных градациях i=0:(Tdiap-1) % исследуем спектр колебаний |
|
N=1024 |
% Длина блока, допустимого по ограничениям памяти |
|
tt=35*10^(-6); |
% Длина токовой фазы |
|
pp0=3*tt; |
% Длина бестоковой фазы при нулевой температуре |
|
fd=8000; |
% Частота дискретизации для имитации осцилограммы |
|
fs=fd/2; |
% Частота Найквиста |
|
step=1/fd; |
% Интервал дискретизации |
|
t=0:step:step*(N-1); |
% Массив временных отсчетов |
|
at=length(t); |
% Его длина |
|
yy=[]; |
% Инициализация массива данных процесса |
|
for ts=0:(Tdiap-1) |
% Начало цикла по температуре |
|
pp=(1-sens*ts)*pp0; |
% Изменяем настройку |
|
y=dtmp(t+rand); |
% Моделируем блок данных от генератора со |
|
% случайной фазой |
|
|
yy=[yy,y]; |
% Добавляем его в массив |
|
end |
% Конец цикла по температуре |
|
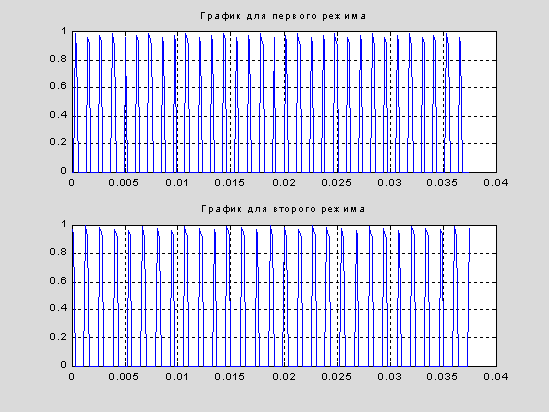
subplot(2,1,1), plot(t(1:N),yy(1:N,1)),title(' График для первого режима '), grid subplot(2,1,2), plot(t(1:N),yy(1:N,2)),title(' График для второго режима '), grid |
|
|
gg=floor(log(at)/log(2)); |
% gg - наименьший показатель степени, для которой |
|
% 2^gg укладывается на считанном блоке отсчетов |
|
|
ffl=2^(gg+1); |
% Длина FFT, возможно, с дополнительными нулями |
|
rr=1:ffl/2; |
% Берем значимую область частот |
|
% удаляя симметричные данные |
|
|
rr=rr(:); |
% Преобразуем в вектор-колонку |
|
lr=length(rr); |
% Длина этого вектора |
|
axe=2:lr; |
% Это нужно для удаления нулевой компоненты |
|
aftt=[]; |
% Инициализация массива мощностей частотных компонент |
|
q12=[]; |
% Инициализация массива мощностей и |
|
% номеров частотных компонент |
|
|
yy=[]; |
% Инициализация массива данных ряда |
|
for ts=0:(Tdiap-1) |
% Начало цикла по температуре |
|
pp=(1-sens*ts)*pp0 |
% Изменяем настройку |
|
y=dtmp(t+rand); |
% Моделируем блок данных от генератора |
|
yy=[yy,y]; |
% Добавляем его в массив |
|
ft=fft(y,ffl); |
% Находим Фурье-представление данных |
|
rr=ft(axe); |
% Удалим нулевую компоненту спектра |
|
pow=rr.*conj(rr); |
% Находим мощности спeктральных компонент |
|
aftt=[aftt,pow]; |
% Добавляем вектор мощностей спектра в массив afft |
|
% для построения графика |
|
|
[q1,q2]=sort(pow); |
% Сортируем pow по возрастанию мощностей, |
|
% сохраняя номера в q2 |
|
|
q12=[q12,q1,q2]; |
% Добавим в q12 номера и энергии ведущих |
|
% компонент |
|
|
end |
% Конец цикла по температуре |
|
nmax=q12(lr-1:-1:lr-6,:); |
% Массив номеров и энергий |
|
% максимальных спектральных компонент |
|
|
subplot(2,1,1), plot(t(1:N),yy(1:N,1)),title(' График для первого режима '), grid |
|
|
subplot(2,1,2), plot(t(1:N),yy(1:N,2)),title(' График для второго режима '), grid |
|
|
subplot(2,1,1), plot(axe*fd/ffl,aftt(:,1)),title(' Спектр для первого режима '), grid |
|
|
subplot(2,1,2), plot(axe*fd/ffl,aftt(:,2)),title(' Спектр для второго режима '), grid |
|
|
disp(['Цена деления по шкале частот=', num2str(fd/lr)]); |
|
|
disp(['Частота Найквиста=', num2str(fs)]); |
|
|
disp(['Мощности и номера ведущих спектральных компонент']); |
|
|
nmax |
|
|
disp(['Ведущие спектральные частоты (гц) ']); |
|
|
fmax=fd/ffl*nmax(:,2:2:2*Tdiap) |
% Переводим номера ведущих |
|
% компонент в соответствующие частоты |
|
И вот что получается при выполнении скрипта:
Tdiap =
2
fs =
4000
pp =
1.0500e-004
pp =
1.0290e-004
Цена деления по шкале частот=31.25
Частота Найквиста=4000
Мощности и номера ведущих спектральных компонент
nmax =
1.0e+003 *
3.9926 0.0550 4.2701 0.0480
1.8613 0.1100 2.0172 0.0960
1.6668 0.0540 1.5181 0.0470
1.3838 0.0010 1.4645 0.0010
1.1451 0.1090 0.9025 0.0950
0.6819 0.0560 0.8621 0.0490
Ведущие спектральные частоты (гц)
fmax =
1.0e+003 *
0.8594 0.7500
1.7188 1.5000
0.8438 0.7344
0.0156 0.0156
1.7031 1.4844
0.8750 0.7656
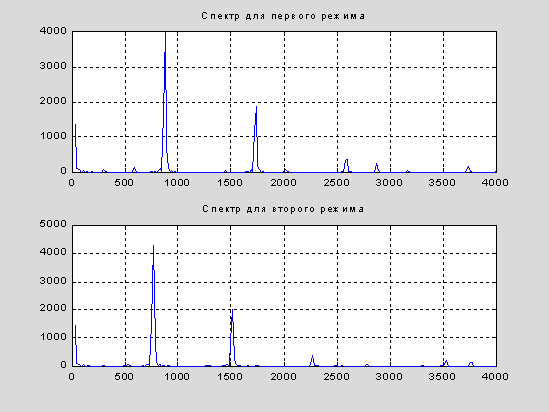
Как видно из графиков и таблиц, можно попробовать разделить сигналы, порожденные работой приборов в различных режимах с помощью полосовых фильтров, полоса пропускания которых находится в пределах [800,900] и [1450,1550] герц для первого и второго режимов соответственно. При этом нужно будет оценить мощщность блоков, полученных в результате фильтрации сигналов и отнести сигнал к тому из классов, который соответствует номеру фильтра с большей выходной мощностью.
|
format long |
% Результаты вычислений сохраним с двойной точностью |
|
[b1,a1]=butter(5,[800,900]/4000) |
|
|
% Проверим, что фильтр действительно пропускает |
|
|
% значительно лучше первую кривую, чем вторую |
|
|
u=[]; |
% Массив результатов фильтрации |
|
for ts=1:2 |
% Начало цикла по температуре |
|
uu=yy(:,ts); |
% Сигнал в режиме с номером ts |
|
uu=filter(b1,a1,uu); |
|
|
u=[u,uu]; |
|
|
end |
|
|
subplot(2,1,1), plot(t(1:N),u(1:N,1)),title(' График для первого режима '), grid subplot(2,1,2), plot(t(1:N),u(1:N,2)),title(' График для второго режима '), grid |
|
|
% Можно дать и колличественную оценку результату фильтрации |
|
|
id=mean(abs(u)) |
|
|
Напоминание: использованы функции MEAN - "среднее" и ABS - "абс. значение". MEAN(S) вектор-строка средих по колонкам матрицы S. Вот коэффициенты полосового фильтра Баттеруорта пятого порядка. |
|
b1 =
1.0e-006 *
Columns 1 through 4
0.08245334349078 0 -0.41226671745389 0
Columns 5 through 8
0.82453343490777 0 -0.82453343490777 0
Columns 9 through 11
0.41226671745389 0 -0.08245334349078
a1 =
1.0e+002 *
Columns 1 through 4
0.01000000000000 -0.07659493144971 0.28216797587454 -0.65057034774127
Columns 5 through 8
1.03455194518947 -1.18253029911747 0.98325939916969 -0.58765947170449
Columns 9 through 11
0.24224504558982 -0.06249765983888 0.00775504905239
А это средние абсолютные величины результатов прохождения сигналов обоих режимов через первый фильтр.
id =
0.1997 0.0181
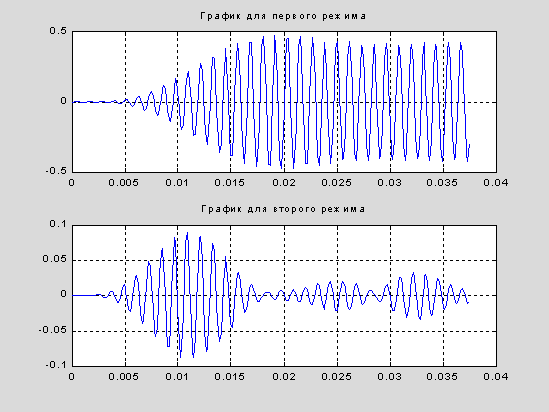
Совершенно аналогично проверяется гипотеза для второй частотной полосы. Таким образом, в результате стендовых расчетов проверяется возможность реализовать алгоритм, а также вычисляются константы, необходимые для преобразования (кодирования) алгоритма в исполняемый модуль.