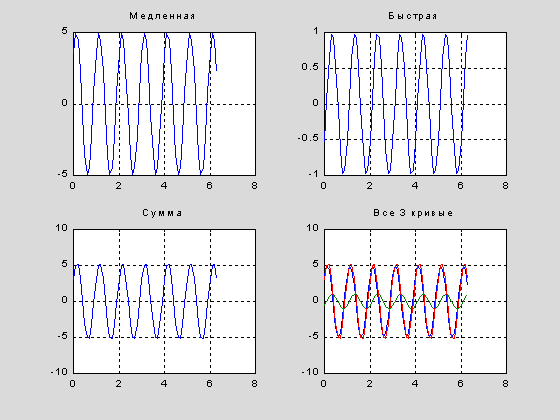
Предположим, что исследуемый процесс является результатом сложения двух гармонических колебаний различной частоты, т.е.
x(t) = медленная_компонента + быстрая_компонента =
= a1*sin(2*pi*om1*(t+R1)) + a2*sin(2*pi*om2*(t+R2)),
где t=k*Dt, k=0,1,...,63, а R1,R2 – случайные величины.
Пусть a1=5, a2=1 om1=1,om2=9 как в Примере 1. При выборе Dt - интервала дискретизации мы продемонстрируемте опасности, которые подстерегают исследователя, занимающегося сбором данных о процессе с целью введения их в ЭВМ для исследования спектра. Вот, наприме, что будет при Dt=0.1 – это отсчетность при которой происходит маскировка быстрой компоненты под медленную.

Построим графики плотности спектра в четырех случаях:
Массив исследуемых значений интервала дискретизации:
clear all
tt=[0.005, 0.015, 0.05 , 0.1];
Соответствующий массив частот Найквиста fc:
ff=1./tt/2
ff =
100.0000 33.3333 10.0000 5.0000
Для всех частот, кроме последней, om1,om2<fc, тогда как в последнем случае om2>fc и om1=2*fc-om2. Это приводит к маскировке частот, т.е. к "исчезновению" быстрой компоненты.
В нижеследующем примере использован цикл for. Он повторяет группу операторов фиксированное, предопределенное число раз. Ключевое слово end очерчивает тело цикла.
В следующем скрипте формируется матрица allfreq, представляющая соответствующие гармонические частоты, т. е. такие частоты, что соответствующие периодические процессы размещают целое число периодов на временном отрезке, в течение которого проходил сбор данных. Матрица мощностей спектра, т.е. амплитуд соотетствующих гармоник, без симметрично-сопряженных данных названа allspectrs. Не поясняем те обозначения, которые уже встречались на стр 39.
**********************
clear all
tt=[0.005, 0.015, 0.05 , 0.1]; a1=5; a2=1;
ff=1./tt/2; N=64; ind=[1:N/2]'; om1=1; om2=9;
alltimes=[];
% Матрица, по колонкам которой соберем временные отметки
allsamples=[];
% Матрица, по колонкам которой соберем отсчеты процессов
allfreq=[];
% Матрица, по колонкам которой соберем гармонические частоты
allspectrs=[];
% Матрица, по колонкам которой соберем соответствующие спектральные
% мощности
for ufh=1:4
t=[0:N-1]'*tt(ufh);
% Вектор значений времени
ts1=a1*sin(2*pi*om1*(t+randn));
% Вектор значений амплитуд медленнной компоненты
ts2=a2*sin(2*pi*om2*(t+randn));
% Вектор значений амплитуд быстрой компоненты
sample=ts1+ts2;
alltimes=[alltimes,t];
allsamples=[allsamples,sample];
freq=(ind-1)*ff(ufh)/32;
% вектор гармонических частот
spectr=abs(fft(sample));
spectr=spectr(ind);
allfreq=[allfreq,freq];
allspectrs=[allspectrs,spectr];
end
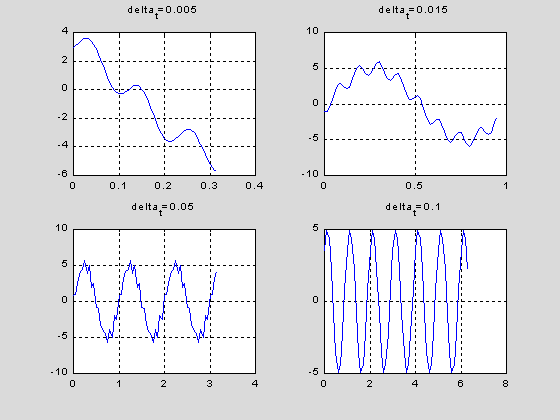
Теперь построим графики зависимостей отсчетов от времени на каждой из временных решеток
subplot(221), plot(alltimes(:,1),allsamples(:,1)), grid, title('delta_t=0.005'),
subplot(222), plot(alltimes(:,2),allsamples(:,2)), grid, title('delta_t=0.015'),
subplot(223), plot(alltimes(:,3),allsamples(:,3)), grid, title('delta_t=0.05'),
subplot(224), plot(alltimes(:,4),allsamples(:,4)), grid, title('delta_t=0.1')
И вот теперь как выглядят графики зависимостей мощности спектра от частоты гармоники
subplot(221), plot(allfreq(:,1),allspectrs(:,1)), grid, title('delta_t=0.005'),
subplot(222), plot(allfreq(:,2),allspectrs(:,2)), grid, title('delta_t=0.015'),
subplot(223), plot(allfreq(:,3),allspectrs(:,3)), grid, title('delta_t=0.05'),
subplot(224), plot(allfreq(:,4),allspectrs(:,4)), grid, title('delta_t=0.1')
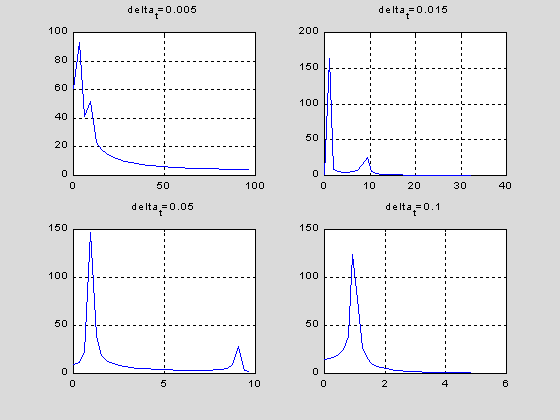
Как видим, первый и последний графики показывают неадекватное представление данных при дискретизации. Причины этих явления различны: для первого графика наблюдается "смешение" низкочастотной компоненты с постоянной составляющей – цена деления Df по оси частот в этом случае равна fc/32= 100/32 и превосходит om1=1. Таким образом, проявляется опасность увлечения высокими частотами Найквиста. Для четвертого графика объяснение прямо следует из теорем о представлении непрерывных данных с помощью дискретных отсчетов.
Замечание. Точка с запятой после выражения в теле цикла предотвращает повторения вывода результатов на экран, а после цикла вывод формируется окончательно. Хорошим стилем являются отступы при использовании циклов для лучшей читаемости, особенно, когда они вложенные.