MATLAB - это высокопроизводительный язык для технических расчетов. Он включает в себя вычисления, визуализацию и программирование в удобной среде, где задачи и решения выражаются в форме, близкой к математической. Типичное использование MATLAB - это:
• математические вычисления;
• создание алгоритмов;
• моделирование;
• анализ данных, исследования и визуализация;
• научная и инженерная графика;
• разработка приложений, включая создание графического интерфейса.
MATLAB - это интерактивная система, в которой основным элементом данных является массив. Это позволяет решать различные задачи, связанные с техническими вычислениями, особенно в которых используются матрицы и вектора, в несколько раз быстрее, чем при написании программ с использованием "скалярных" языков программирования, таких как Си или Фортран.
Слово MATLAB означает матричная лаборатория (matrix laboratory). MATLAB был специально написан для обеспечения легкого доступа к LINPACK и EISPACK, которые представляют собой современные программные средства для матричных вычислений.
MATLAB развивался в течение нескольких лет, ориентируясь на различных пользователей. В университетской среде, он представлял собой стандартный инструмент для работы в различных областях математики, машиностроении и науки. В промышленности, MATLAB — это инструмент для высокопродуктивных исследований, разработок и анализа данных.
В MATLAB важная роль отводится специализированным группам программ, называемых toolboxes. Они очень важны для большинства пользователей MATLAB, так как позволяют изучать и применять специализированные методы. Toolboxes - это всесторонняя коллекция функций MATLAB (М-файлов), которые позволяют решать частные классы задач. Toolboxes применяются для обработки сигналов, систем контроля, нейронных сетей, нечеткой логики, волновых пакетов (wavelets), моделирования и т.д.
Система MATLAB состоит из пяти основных частей:
Язык MATLAB. Это язык матриц и массивов высокого уровня с управлением потоками, функциями, структурами данных, вводом-выводом и особенностями объектно-ориентированного программирования. Это позволяет, как программировать в "небольшом масштабе" для быстрого создания черновых программ, так и в "большом" для создания больших и сложных приложений.
Среда matlab. Это набор инструментов и приспособлений, с которыми работает пользователь или программист MATLAB. Она включает в себя средства для управления переменными в рабочем пространстве MATLAB, вводом и выводом данных, а также создания, контроля и отладки М-файлов и приложений MATLAB.
Управляемая графика. Это графическая система MATLAB, которая включает в себя команды высокого уровня для визуализации двух- и трехмерных данных, обработки изображений, анимации и иллюстрированной графики. Она также включает в себя команды низкого уровня, позволяющие полностью редактировать внешний вид графики, также как при создании графического Пользовательского Интерфейса (GUI) для MATLAB приложений.
Библиотека математических функций. Это обширная коллекция вычислительных алгоритмов от элементарных функций, таких как сумма, синус, косинус, комплексная арифметика, до более сложных, таких как обращение матриц, нахождение собственных значений, функции Бесселя, быстрое преобразование Фурье.
Программный интерфейс. Это библиотека, которая позволяет писать программы на Си и Фортране, которые взаимодействуют с MATLAB. Она включает средства для вызова программ из MATLAB (динамическая связь), вызывая MATLAB как вычислительный инструмент и для чтения-записи МАТ-файлов.
Simulink, сопутствующая MATLAB программа, - это интерактивная система для моделирования нелинейных динамических систем. Она представляет собой среду, управляемую мышью, которая позволяет моделировать процесс путем перетаскивания блоков диаграмм на экране и их манипуляцией. Simulink работает с линейными, нелинейными, непрерывными, дискретными, многомерными системами.
Blocksets - это дополнения к Simulink, которые обеспечивают библиотеки блоков для специализированных приложений, таких как связь, обработка сигналов, энергетические системы.
Real-Time Workshop - это программа, которая позволяет генерировать С-код из блоков диаграмм и запускать их на выполнение на различных системах реального времени.
Эта книга предназначена для начального освоения и изучения MATLAB. Она содержит некоторое количество примеров, которые могут быть запущены и отслежены в MATLAB. Чтобы запустить MATLAB на PC дважды щелкните на иконку MATLAB. Для выхода из MATLAB необходимо набрать quit в строке MATLAB или использовать обычное сочетание клавиш Alt-F4. Если вам необходимо получить дополнительную информацию, наберите help в строке MATLAB или выберите Help в меню. Мы более подробно расскажем вам об этом позднее. Лучший способ начать работу с MATLAB — это научиться обращаться с матрицами. В этой главе мы покажем вам, как надо это делать. В MATLAB матрица - это прямоугольный массив чисел. Особое значение придается матрицам 1х1, которые являются скалярами, и матрицам, имеющим один столбец или одну строку, — векторам. MATLAB использует различные способы для хранения численных и не численных данных, однако вначале лучше всего рассматривать все данные как матрицы. MATLAB организован так, чтобы все операции в нем были как можно более естественными. В то время как другие программные языки работают с числами как элементами языка, MATLAB позволяет вам быстро и легко оперировать с целыми матрицами.
Переменным присваивают числовые значения, печатая выражение непосредственно, например, печатая
> a = 1+2
Вы получите
а =
3
Ответ не будет отображен, если точка с запятой помещена в конце выражения, например, напечатайте a=1+2;.
Переменную можно определить, используя, эти операторы, числа или предварительно определенные переменные. Например, поскольку a уже определено, следующее выражение имеет силу
B = 2*a
Чтобы получить значение предварительно определенной переменной, напечатайте соответствующий символ:
B
даст
B =
6
Имеются несколько предопределенных переменных, которые могут использоваться в любое время, тем же самым способом как определяемые пользователем переменные:
i Sqrt (-1)
j Sqrt (-1)
pi 3.1416 ...
Например, вызов
Y = 2 * (1+4*j)
дает:
Y =
2.0000 + 8.0000i
Имеется также множество предопределенных (built-in) функций, которые могут использоваться при определении переменной. Некоторые обычные функции, которые используются в этом тексте:
abs модуль комплексного числа или абсолютное значение для вещественного
angle аргумент комплексного числа, в радианах
cos Функция косинуса, (предполагается, что аргумент выражен в радианах)
sin Функция синуса, (предполагается, что аргумент выражен в радианах)
exp показательная функция
Например, с y, определенным выше, вызывая
> C = abs (y)
получим: C =
8.2462
C = angle(y)
получим: C =
1.3258
Если a=3 как определено предварительно,
C = cos(a)
получим: C =
-0.9900
C = exp (a)
получим: C =
20.0855
Обратите внимание, что exp может использоваться с комплексным аргументом. Например, с y = 2+8i, как определено выше,
C = exp (y)
получим: C =
-1.0751 + 7.3104i
Вы можете вводить матрицы в MATLAB несколькими способами:
• вводить полный список элементов;
• загружать матрицы из внешних файлов;
• генерировать матрицы, используя встроенные функции;
• создавать матрицы с помощью ваших собственных функций в М-файлах.
Чтобы ввести матрицу можно:
• отделять элементы строки пробелами или запятыми
• использовать точку с запятой, ;, для обозначения окончания каждой строки
• окружать весь список элементов квадратными скобками, [ ]. Чтобы ввести матрицу Дюрера просто напишите:
А = [16 3 2 13; 5 10 11 8; 9 6 7 12; 4 15 14 1]
MATLAB отобразит матрицу, которую мы ввели:
А =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
Это точно соответствует числам на гравюре. Если мы ввели матрицу, то она автоматически запоминается средой MATLAB. И мы можем к ней легко обратиться как к А. Сейчас, когда мы имеем А в рабочем пространстве MATLAB, посмотрим, что делает её такой интересной. Почему она называется магической?
Вы возможно уже знаете, что особые свойства магического квадрата связаны с различными способами суммирования его элементов. Если вы берёте сумму элементов вдоль какой-либо строки или столбца, или вдоль какой-либо из двух главных диагоналей, вы всегда получите одно и тоже число. Давайте проверим это, используя MATLAB. Первое утверждение, которое мы проверим -
sum (A)
MATLAB выдаст ответ
ans =
34 34 34 34
Когда выходная переменная не определена, MATLAB использует переменную ans, коротко от answer - ответ, для хранения результатов вычисления. Мы подсчитали вектор-строку, содержащую сумму элементов столбцов матрицы А. Действительно, все столбцы имеют одинаковую сумму, магическую сумму, равную 34. А как насчет сумм в строках? MATLAB предпочитает работать со столбцами матрицы, таким образом, лучший способ получить сумму в строках — это транспонировать нашу матрицу, подсчитать сумму в столбцах, а потом транспонировать результат. Операция транспонирования обозначается апострофом или одинарной кавычкой. Она зеркально отображает матрицу относительно главной диагонали и меняет строки на столбцы. Таким образом
A'
вызывает ответ
ans =
16 5 9 4
3 10 6 15
2 11 7 14
13 8 12 1
А выражение
sum(A') '
вызывает результат вектор-столбец, содержащий суммы в строках
ans =
34
34
34
34
Сумму элементов на главной диагонали можно легко получить с помощью функции diag, которая выбирает эту диагональ.
diag(B)
ans =
16
11
6
1
А строка
sum (diag (А) )
вызывает
ans =
34
Другая диагональ, называемая побочной, не так важна математически, поэтому MATLAB не имеет специальной функции для неё. А функция flipir зеркально отображает матрицу слева направо. Таким образом,
fliplr(A)
ans =
13 3 2 16
8 10 11 5
12 6 7 9
1 15 14 4
Мы проверили, что матрица на гравюре Дюрера действительно магическая, и научились использовать некоторые матричные операции MATLAB. В последующих разделах мы продолжим использовать эту матрицу для демонстрации дополнительных возможностей MATLAB.
Элемент в строке i и столбце j матрицы А обозначается A(i,j). Например, А(4,2) - это число в четвертой строке и втором столбце. Для нашего магического квадрата А(4,2) =15. Таким образом, можно вычислить сумму элементов в четвертом столбце матрицы А, набрав
А(1,4) + А(2,4) + А(3,4) + А(4,4)
получим
ans =
34
Однако это не самый лучший способ суммирования отдельной строки. Также возможно обращаться к элементам матрицы через один индекс, A(k). Это обычный способ ссылаться на строки и столбцы матрицы. Но его можно использовать только с двумерными матрицами. В этом случае массив рассматривается как длинный вектор, сформированный из столбцов исходной матрицы. Так, для нашего магического квадрата, А(8) - это другой способ ссылаться на значение 15, хранящееся в А(4,2). Если вы пытаетесь использовать значение элемента вне матрицы, MATLAB выдаст ошибку:
t=A(4,5) ??? Index exceeds matrix dimensions.
С другой стороны, если вы сохраняете значение вне матрицы, то размер матрицы увеличивается.
Х=А;
Х(4,5) = 17;
16 2 3 13 0
5 11 10 8 0
9 7 6 12 0
4 14 15 1 17
Двоеточие, ":" , - это один из наиболее важных операторов MATLAB. Он проявляется в различных формах. Выражение
1:10
- это вектор-строка, содержащая целые числа от 1 до 10
1 2 3 4 5 6 7 8 9 10
Для получения обратного отсчета, опишем приращение. Например
100:-7:50
что дает
100 93 86 79 72 65 58 51
или
0:pi/4:pi
что приводит к
Индексное выражение, включая двоеточие, относится к части матрицы.
A(l:k,j) - это первые k элементов j-го столбца матрицы А. Так что
sum(A( 1:4,4))=34.
MATLAB имеет четыре функции, которые создают основные матрицы:
zeros(m,n) mxn - матрица из нулей
ones(m,n) mxn - матрица из единиц
rand(m,n) mxn - матрица из равномерного распределенных на [0,1] случайных чисел
randn(m,n) mxn - матрица - то же с нормальным распределением.
Некоторые примеры:
Z = zeros(2,4)
Z =
0 0 0 0
0 0 0 0
F = 5*ones(3,3)
F =
5 5 5
5 5 5
5 5 5
N = fix(10*rand(l,10))
N =
9 2 6 4 8 7 4 0 8 4
R = randn(4,4)
R=
-0.4326 -1.1465 0.3273 -0.5883
-1.6656 1.1909 0.1746 2.1832
0.1253 1.1892 -0.1867 -0.1364
0.2877 -0.0376 0.7258 0.1139
Команда load считывает двоичные файлы, содержащие матрицы, созданные в MATLAB ранее, или текстовые файлы, содержащие численные данные. Текстовые файлы должны быть сформированы в виде прямоугольной таблицы чисел, отделенных пробелами, с равным количеством элементов в каждой строке. Например, создадим вне MATLAB текстовой файл, содержащий 4 строки:
16.0 3.0 2.0 13.0
5.0 10.0 11.0 8.0
9.0 6.0 7.0 12.0
4.0 15.0 14.0 1.0
Сохраним этот файл под именем magik.dat. Тогда команда
load magik.dat
прочитает этот файл и создаст переменную magik, содержащую нашу матрицу.
Объединение - это процесс соединения маленьких матриц для создания больших. Фактически, вы создали вашу первую матрицу объединением её отдельных элементов. Пара квадратных скобок - это оператор объединения. Например, начнем с матрицы А (магического квадрата 4х4) и сформируем
В = [А А+32; А+48 А+16]
Результатом будет матрица 8х8, получаемая соединением четырех подматриц
B =
16 2 3 13 48 34 35 45
5 11 10 8 37 43 42 40
9 7 6 12 41 39 38 44
4 14 15 1 36 46 47 33
64 50 51 61 32 18 19 29
53 59 58 56 21 27 26 24
57 55 54 60 25 23 22 28
52 62 63 49 20 30 31 17
Это матрица лишь наполовину является магической. Её элементы представляют собой комбинацию целых чисел от 1 до 64, а суммы в столбцах точно равны значению для магического квадрата 8х8.
sum (В)
ans =
260 260 260 260 260 260 260 260
Однако, суммы в строках этой матрицы ( sum(B')' ) не все одинаковы. Необходимо провести дополнительные операции, чтобы сделать эту матрицу действительно магическим квадратом 8х8.
Вы можете удалять строки и столбцы матрицы, используя просто пару квадратных скобок. Пусть
Х = А;
Теперь удалим второй столбец матрицы X.
X(:,2) = [].
Эта операция изменит Х следующим образом
X =
16 3 13 5
10 8 9 6
12 4 15 1
Если вы удаляете один элемент матрицы, то результат уже не будет матрицей. Так выражение
Х(1,2)=[]
результатом вычисления выдаст ошибку. Однако использование одного индекса удаляет отдельный элемент или последовательность элементов и преобразует оставшиеся элементы в вектор-строку. Так
X(2:2:10) = []
выдаст результат
X =
16 9 3 6 13 12 1
Как и большинство других языков программирования, MATLAB предоставляет возможность использования математических выражений, но в отличие от многих из них, эти выражения в MATLAB включают матрицы. Основные составляющие выражения:
• переменные
• числа
• операторы
• функции
Переменные. В MATLAB нет необходимости в определении типа переменных или размерности. Когда MATLAB встречает новое имя переменной, он автоматически создает переменную и выделяет соответствующий объем памяти. Если переменная уже существует, MATLAB изменяет ее состав и если это необходимо выделяет дополнительную память. Например,
num_students = 25
создает матрицу 1х1 с именем num_students и сохраняет значение 25 в ее единственном элементе. Имена переменных состоят из букв, цифр или символов подчеркивания. MATLAB использует только первые тридцать один символ для имени переменной. MATLAB чувствителен к регистрам, он различает заглавные и строчные буквы. Поэтому А и а - не одна и та же переменная. Чтобы увидеть матрицу, связанную с переменной, просто введите название переменной. Числа. MATLAB использует принятую десятичную систему счисления, с необязательной десятичной точкой и знаками плюс-минус для чисел. Научная система счисления использует букву е для определения множителя степени десяти. Мнимые числа используют i или j как суффикс. Некоторые примеры правильных чисел приведены ниже
| 3 |
-99 |
0.0001 |
| 9.6397238 |
1.60210е-20 |
6.02252е23 i |
| 1i |
-3.14159j |
3e5i |
Все числа для хранения используют формат long, определенный стандартом плавающей точки IEEE. Числа с плавающей точкой обладают ограниченной точностью - приблизительно 16 значащих цифр и ограниченным диапазоном -приблизительно от 10308 до 10308
Операторы. Выражения используют обычные арифметические операции и правила старшинства, используя скобки в случае необходимости.
Функции. MATLAB предоставляет большое количество элементарных математических функций, таких как abs, sqrt, exp, sin. Вычисление квадратного корня или логарифма отрицательного числа не является ошибкой: в этом случае результатом является соответствующее комплексное число. MATLAB также предоставляет и более сложные функции, включая Гамма функцию и функции Бесселя. Большинство из этих функций имеют комплексные аргументы. Чтобы вывести список всех элементарных математических функций, наберите
help elfun. Для вывода более сложных математических и матричных функций, наберите, например, help specfun или help elmat соответственно. Некоторые функции, такие как sqrt и sin, - встроенные. Они являются частью MATLAB, поэтому они очень эффективны, но их вычислительные детали трудно доступны. В то время как другие функции, такие как gamma и sink, реализованы в М-файлах. Поэтому вы можете легко увидеть их код и, в случае необходимости, даже модифицировать его.
Несколько специальных функций предоставляют значения часто используемых констант.
pi 3.14159265...
i мнимая единица ![]() ,
,
j то же самое, что и i
eps относительная точность числа с плавающей точкой, ![]()
realmin наименьшее число с плавающей точкой, ![]()
realmax наибольшее число с плавающей точкой, ![]()
Inf бесконечность
NaN не число
Бесконечность появляется при делении на нуль или при выполнении математического выражения, приводящего к переполнению, т.е. к превышению realmax. Не число (NaN) генерируется при вычислении выражений типа 0/0 или Inf- Inf, которые не имеют определенного математического значения.
Имена функций не являются зарезервированными, поэтому возможно изменять их значения на новые, например
eps = l.e-6
и далее использовать это значение в последующих вычислениях. Начальное значение может быть восстановлено следующим образом
clear eps
Выражения Вы уже познакомились с некоторыми примерами использования выражений в MATLAB. Ниже приведено еще несколько примеров с результатами.
rho = (l+sqrt(5))/2
rho =
1.6180
a = abs(3+4i)
a =
5
z = sqrt(besselk(4/3,rho-i))
z =
0.3730 + 0.32141
huge = exp(log(realmax))
huge = 1.7977e+308
toobig = pi*huge
toobig = Inf
Бинарные операции, которые должны быть выполнены " элемент за элементом " отмечают при помощи символа, ". " предшествующего знаку операции. Например, чтобы получить вектор x, который содержит элементы x (t) = tcos (t) в определенных точках во времени. Вы можете просто соединить вектор t с векторным cos(t) знаком умножения с предшествующей точкой:
t = 0:10; x = t.*cos (t).
Вы можете создавать свои собственные матрицы, используя М-файлы, которые представляют собой текстовые файлы, содержащие код MATLAB. Просто создайте файл с выражением, которое вы хотите написать в командной строке MATLAB. Сохраните его под именем c расширением m. В качестве примера М-файла, который определяет функцию, создайте файл в вашем рабочем каталоге, названном yplusx.m, который содержит следующие команды:
function z = yplusx(y,x)
z = y + x;
Следующие команды, напечатанные в командном окне MATLAB'а демонстрируют, как этот М-файл используется:
x = 2;
y = 3;
z = yplusx(y,x)
М-файлы наиболее эффективны, когда написаны c целью использования матричных или векторных операции. Циклы и условные операторы доступны, но должны использоваться экономно, так как они в вычислительном отношении неэффективны. Пример использования команды for
for k=1:10,
x(k) = cos(k);
end
Это создает 1x10 вектор x содержащий косинусы положительных целых чисел от 1 до 10. Эта операция выполнена более эффективно с командами k = 1:10; X = cos(k); которые использует функцию векторного присваивания вместо for-цикла. Условный оператор может использоваться, чтобы определить условные инструкции. Пример
if(a <= 2),
b = 1;
elseif(a >=4)
b = 2;
else
b = 3;
end
Допустимые сравнения между выражениями таковы : > =, <=, =, <,>, ==, и ~ =.
Дополнительная информация в М-файл, определяемая пользователем, может быть введена при помощи команды input. Например, предположим, что Вы хотите выполнить М-файл с различными значениями переменной T. Следующая командная строка в пределах М-файла определяет значение:
T = input('Input the value of T: ')
Любой комментарий, заключенный между кавычками, будет отображен на экране, когда М-файл выполняется, и пользователь должен ввести соответствующее значение.
Замечание. Для вызова текстового редактора на PC, выберите Open или New из меню File или нажмите соответствующую кнопку на панели инструментов. Возможно также управление доступом к редактору с помощью командной строки edit [<имя_файла>].
Например, создадим файл, включающий следующие 5 строк:
А=[...
16.0 3.0 2.0 13.0
5.0 10.0 11.0 8.0
9.0 6.0 7.0 12.0
4.0 15.0 14.0 1.0 ];
Сохраним его под именем magik.m. Тогда выражение
magik
прочитает файл и создаст переменную А, содержащую исходную матрицу.
До сих пор, мы использовали только командную строку MATLAB, печатая команды и выражения и наблюдая результаты. В этой главе описано несколько способов изменения внешнего вида командного окна. Если ваша система позволяет вам выбирать шрифт, то мы рекомендуем использовать шрифты с фиксированной шириной, такие как Fixedsys или Courier, для обеспечения правильного межстрочного интервала.
Команда format. Команда format управляет численным форматом значений, выводимых MATLAB. Эта операция влияет только на то, как числа изображаются на экране, но не влияет на то, как их вычисляет и сохраняет MATLAB. Ниже представлены различные форматы чисел, используемые для отображения вектора х с компонентами различных величин.
х = [4/3 1.2345е-6]
format short
0.0000
format short e
1.3333e+000 1.2345e-006
format short g 1.3333 1.2345e-006
format long
1.33333333333333 0.00000123450000
format long e
1.333333333333333e+000 1.23450000000000Oe-006
format long g
1.33333333333333 1.2345e-006
format bank
1.33 0.00
format rat
4/3 1/810045
format hex
3ff5555555555555 3eb4b6231abfd271
Если самый большой элемент матрицы больше 103 или самый маленький меньше ![]() , MATLAB применяет общий масштабный коэффициент для форматов short и long. В добавление к командам format, рассмотренным выше
, MATLAB применяет общий масштабный коэффициент для форматов short и long. В добавление к командам format, рассмотренным выше
format compact убирает много пустых линий, появляющихся на выходе. Это позволяет вам видеть больше информации на экране. Если вы хотите изменить контроль над форматом выходных данных, используйте функции sprintf и fprintf.
Сокращение выходных данных Если вы наберете выражение и нажмете Return или Enter, MATLAB автоматически выведет результат на экран. Однако если в конце строки вы поставите точку с запятой, MATLAB проведет вычисления, но не отобразит их. Это часто бывает нужно при создании больших матриц.
Длинные командные строки. Если выражение не умещается на одной строке, используйте троеточие, а за ним Return или Enter, для обозначения того, что выражение продолжается на следующей строке. Например
s = 1 -1/2 + 1/3 -1/4 + 1/5 - 1/6 + 1/7 ...
-1/8 + 1/9 - 1/10 + 1/11 - 1/12;
Пробелы вокруг знаков =, +, - не обязательны, но улучшают читаемость текста. Редактор командной строки Различные стрелки и управляющие клавиши на вашей клавиатуре позволяют вам вызывать, редактировать и многократно использовать команды, набранные ранее. Например, предположим, что вы допустили ошибку при вводе
rho = (1 + sqt(5))/2
Вы ошиблись в написании sqrt. MATLAB ответит вам предупреждением Undefined function or variable 'sqt'.
Вместо того, чтобы заново набирать всю строку, просто нажмите клавишу ![]() . Тогда на экране изобразится ошибочная команда. Используйте клавишу <— для перемещения курсора и вставки пропущенной буквы r. Повторное использование клавиши
. Тогда на экране изобразится ошибочная команда. Используйте клавишу <— для перемещения курсора и вставки пропущенной буквы r. Повторное использование клавиши ![]() вызовет предыдущие строки. Наберите несколько символов, и тогда клавиша
вызовет предыдущие строки. Наберите несколько символов, и тогда клавиша ![]() найдет предыдущую строку, которая начинается с них. Список доступных клавиш редактирования в командной строке отличается у разных компьютеров. Поэкспериментируйте, чтобы узнать, какие из клавиш доступны на вашей машине.
найдет предыдущую строку, которая начинается с них. Список доступных клавиш редактирования в командной строке отличается у разных компьютеров. Поэкспериментируйте, чтобы узнать, какие из клавиш доступны на вашей машине.
MATLAB имеет широкие возможности для графического изображения векторов и матриц, а также для создания комментариев и печати графики. Эта глава описывает несколько наиболее важных графических функций и дает примеры их применения.
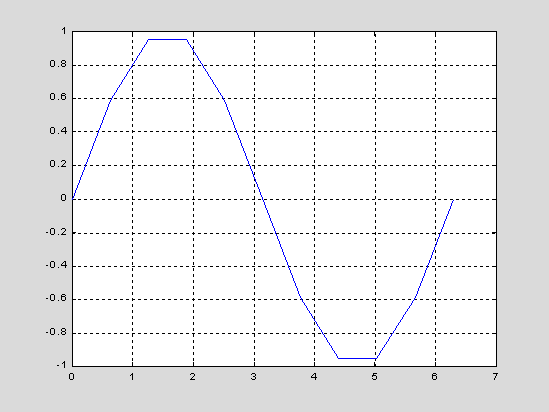
Функция plot имеет различные формы, связанные с входными параметрами, например plot(y) создает кусочно-линейный график зависимости элементов у от их индексов. Если вы задаете два вектора в качестве аргументов, plot(x,y) создаст график зависимости у от х. Например, для построения графика значений функции sin от нуля до 2л, сделаем следующее
y = sin(t) ;
plot (t,y), grid
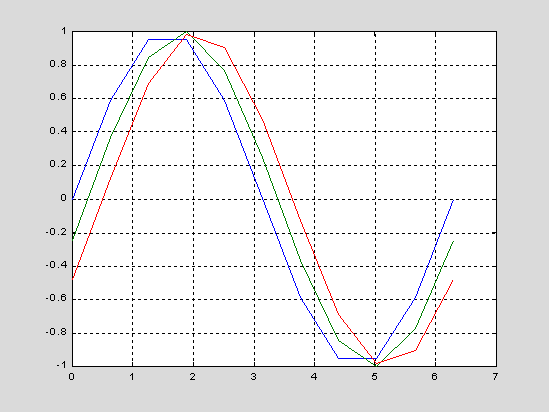
Вызов функции plot с многожественными парами х-у создает многочисленные графики. MATLAB автоматически присваивает каждому графику свой цвет (исключая случаи, когда это делает пользователь), что позволяет различать заданные наборы данных. Например, следующие три строки отображают график близких функций, и каждой кривой соответствует свой цвет:
y3 = sin(t-.5);
plot( t, y, t, y2, t, y3),grid
Возможно изменение цвета, стиля линий и маркеров, таких как знаки плюс или кружки, следующим образом
plot(x, у, 'цвет_стиль_маркер')
гду цвет_стиль_маркер это одно-, двух- или трехсимвольная строка (заключенная в одинарные кавычки), составленная из типов цвета, стиля линий и маркеров:
• Символы, относящие к цвету: 'c', 'm', 'у', 'г', 'g', 'b, 'w' и 'k'. Они обозначают голубой, малиновый, желтый, красный, зеленый, синий, белый и черный цвета соответственно.
• Символы, относящиеся к типу линий: ' - ' для сплошной, ' - - ' для разрывной, '; ' для пунктирной, ' -. ' для штрихпунктирной линий и ' none ' для её отсутствия.
• Наиболее часто встречающиеся маркеры '+ ', ' о ', ' * ' и ' х '.
Например, выражение plot(t,y,'y:+') строит черный пунктирный график и помещает маркеры ' + 'в каждую точку данных. Если вы определяете только тип маркера, но не определяете тип стиля линий, то MATLAB выведет только маркеры.
Функция plot автоматически открывает новое окно изображения (далее окно), если до этого его не было на экране. Если же оно существует, то plot использует его по умолчанию. Для открытия нового окна и выбора его по умолчанию, наберите
figure
Для того, чтобы сделать существующее окно текущим –
figure(n)
где n - это номер в заголовке окна. В этом случае результаты всех последующих команд будут выводиться в это окно.
Добавление кривых на существующий график. Команда hold позволяет добавлять кривые на существующий график. Когда вы набираете
hold on
MATLAB не стирает существующий график, а добавляет в него новые данные, изменяя оси, если это необходимо.
Подграфики. Функция subplot позволяет выводить множество графиков в одном окне или распечатывать их на одном листе бумаги.
subplot(m,n,p)
разбивает окно изображений на матрицу m на п подграфиков и выбирает р-ый подграфик текущим. Графики нумеруются вдоль первого в верхней строке, потом во второй и т.д.
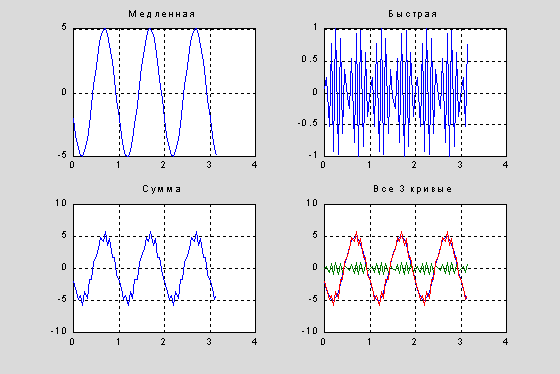
Получить графические представления данных наблюдения периодических процессов при различных соотношениях составляющих частот и представить графические данные в четырех разных подобластях окна:
om1=1; a1=5; % Частота и амплитуда медленной компоненты
om2=9; a2=1; % Частота и амплитуда быстрой компоненты
N=64; % Длина блока данных
delta_t=0.05; % Шаг по оси времен
allt=(N-1)*delta_t; % Длительность наблюдения
t=0:delta_t:allt; % Вектор значений времени
ts1=a1*sin(2*pi*om1*(t+randn))'; % Вектор значений амплитуд медленнной компоненты
ts2=a2*sin(2*pi*om2*(t+randn))'; % Вектор значений амплитуд быстрой компоненты
ts1s=ts1+ts2; % Вектор значений амплитуд результирующего процесса
subplot(221), plot(t,ts1), grid, title('Медленная')
subplot(222), plot(t,ts2), grid,title('Быстрая')
subplot(223), plot(t,ts1s), grid,title('Сумма')
subplot(224), plot(t,[ts1,ts2,ts1s]), grid,title('Все 3 кривые')
Мнимые и комплексные данные. Если аргумент функции plot комплексное число, то мнимая часть игнорируется, за исключением случая, когда комплексный аргумент один. Для этого специального случая происходит построение графика зависимости реальной части аргумента от мнимой. Поэтому
plot(Z)
где Z комплексный вектор или матрица, эквивалентно plot(real(Z) ,imag(Z))
Например,
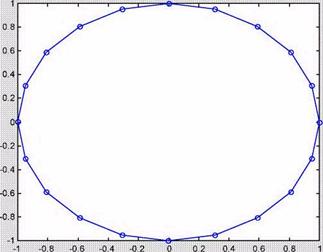
t = 0:pi/l0:2*pi;
plot(exp(i*t),'-о')
отобразит двадцатисторонний многоугольник с маленькими кружками на вершинах.
Управление осями. Функция axis имеет несколько возможностей для настройки масштаба, ориентации и коэффициента сжатия. Обычно MATLAB находит максимальное и минимальное значение и выбирает соответствующий масштаб и маркитирование осей. Функция axis заменяет значения по умолчанию предельными значения, вводимыми пользователем.
axis( [xmin xmax ymin ymax])
В функции axis можно также использовать ключевые слова для управления внешним видом осей. Например
axis square
создает х и у оси равной длины, а
axis equal
создает отдельные отметки приращений для х и у осей одинаковой длины. Так, функция
plot(exp(i*t))
следующая либо за axis square, либо за axis equal превращает овал в правильный круг.
axis auto
возвращает значения по умолчанию и переходит в автоматический режим.
axis on
включает обозначения осей и метки промежуточных делений.
axis off выключает обозначения осей и метки промежуточных делений.
grid off выключает сетку координат, а
grid on включает её заново.
Подписи к осям и заголовки. Функции xlabel, ylabel, zlabel добавляют подписи к соответствующим осям, функция title добавляет заголовок в верхнюю часть окна, а функция text вставляет текст в любое место графика. Использование синтаксических соглашений, принятых в ТЕХ, позволяет применять греческие буквы, математические символы и различные шрифты. Следующий пример демонстрирует эту возможность.
loo=20;
t = -pi:pi/loo:pi;
y = sin(t);
plot (t, y)
grid
axis ([-pi pi -1 1])
xlabel( ' -\pi \leq \itt \leq \pi ' )
ylabel( ' sin(t) ' )
title( ' График функции sin ' )
text(-l, -1/3, ' \it{Oтметьте нечетную симметрию} ' )
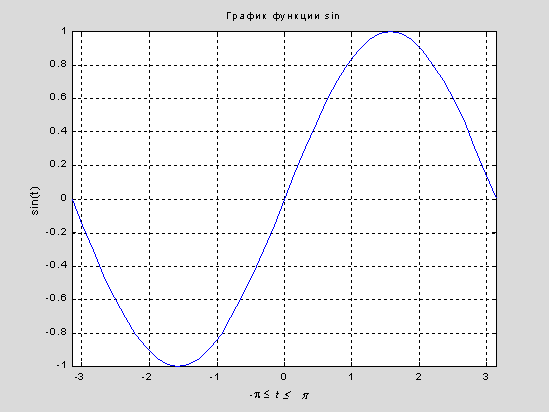
Печать графики.. Опция Print в меню File и команда print печатают графику MATLAB. Меню Print вызывает диалоговое окно, которое позволяет выбирать общие стандартные варианты печати. Команда print обеспечивает большую гибкость при выводе выходных данных и позволяет контролировать печать из М-файлов. Результат может быть послан прямо на принтер, выбранный по умолчанию, или сохранен в заданном файле. Возможно широкое варьирование формата выходных данных, включая использование PostScript.
Есть несколько способов получить текущую документацию по функциям MATLAB.
• Команда help
• Окно справки
• MATLAB Help Desk
• Текущие справочные страницы
• Связь с The MathWorks, Inc.
Команда help
Команда help - это самый основной способ определения синтаксиса и поведения отдельных функций. Информация отображается прямо в командном окне. Например
help randn
выдаст
S = RANDN('state') is a 2-element vector containing the current state
……………………………………………………………………….
RANDN('state',J) and RANDN('state',S) cause the MATLAB 5 generator
to be used.
See also RAND, SPRAND, SPRANDN, RANDPERM.
Замечание. MATLAB в текущей справке использует заглавные буквы для функций и переменных для того, чтобы выделить их из текста. Однако, при наборе имен функций всегда используйте соответствующие строчные буквы, так как MATLAB чувствителен к регистрам, а все имена функции строчные.
Все функции MATLAB организованы в логические группы и структура директорий MATLAB базируется на этом группировании. Например, все функции линейной алгебры находятся в директории matfun. Чтобы вывести имена всех функций в этой директории с кратким описанием, надо набрать
help matfun
Ответ будет содержать пару экранов текста типа:
Matrix functions - numerical linear algebra.
Matrix analysis.
norm - Matrix or vector norm.
……………………………………………..
Linear equations.
\ and / - Linear equation solution; use "help slash".
inv - Matrix inverse.
……………………………………………..
Eigenvalues and singular values.
eig - Eigenvalues and eigenvectors.
svd - Singular value decomposition.
……………………………………………..
Matrix functions.
expm - Matrix exponential.
……………………………………………..
Factorization utilities
qrdelete - Delete column from QR factorization.
……………………………………………..
Matrix functions - numerical linear algebra.
Matrix analysis.
norm - Matrix or vector norm.
……………………………………………..
Команда
help matlab\general ( Общецелевые комапнды) выдаст результат типа
General information
help - On-line help, display text at command line.
helpwin - On-line help, separate window for navigation.
……………………………………………..
Managing the workspace.
who - List current variables.
whos - List current variables, long form.
……………………………………………..
Managing commands and functions.
what - List MATLAB-specific files in directory.
type - List M-file.
……………………………………………..
Managing the search path
path - Get/set search path.
addpath - Add directory to search path.
……………………………………………..
Controlling the command window.
echo - Echo commands in M-files.
more - Control paged output in command window.
diary - Save text of MATLAB session.
……………………………………………..
Operating system commands
cd - Change current working directory.
copyfile - Copy a file.
……………………………………………..
Debugging M-files.
debug - List debugging commands.
dbstop - Set breakpoint.
……………………………………………..
Profiling M-files.
profile - Profile function execution time.
help matlab\ops Operators and special characters.
Окно справки MATLAB'а появляется на PC после выбора опции Help Window в меню Help или нажатием кнопки вопроса на панели инструментов. Эта же операция может быть выполнена при наборе команды
helpwin
Для вывода окна справки по отдельным разделам, наберите helpwin topic
Окно справки предоставляет вам такую же информацию, как и команда help, но оконный интерфейс обеспечивает более удобную связь с другими разделами справки. Команда
lookfor
позволяет искать функции по ключевому слову. Она просматривает первую строку текста справки, называемую строкой HI, для каждой функции MATLAB и возвращает строки HI, содержащие заданное ключевое слово. Например, MATLAB не имеет функции с именем inverse. Поэтому ответ на запрос
help inverse
будет
inverse.m not found. В то время как
lookfor inverse
найдет множество согласованных ответов. В зависимости от того, какие toolboxes вы установили, вы получите соответствующие записи. Например
INVHILB Inverse Hilbert matrix.
ACOS Inverse cosine.
ACOSH Inverse hyperbolic cosine.
и т. д.
Добавление ключа -all в команду lookfor, как, например,
lookfor –all inverse
позволяет искать ключевое слово во всех записях справки, а не только в строке HI.
Help Desk обеспечивает доступ к широкому диапазону справочной информации, хранящейся на диске или на CD вашей системы. Большая часть важной документации использует HTML (HyperText Markup Language) формат и доступна через браузеры Интернет, такие как Netscape или Microsoft Explorer. Запустить Help Desk можно на PC, выбрав опцию Help Desk в меню Help или, на всех компьютерах, просто набрав команду
helpdesk
Все операторы и функции MATLAB имеют текущие справочные страницы в формате HTML, к которым можно обратиться через Help Desk. Эти страницы предоставляют больше деталей и примеров, чем обычные записи справки. Также доступны HTML версии и других документов, включая это справочное пособие. Средство поиска, запущенное на вашей машине, может найти все текущие справочные материалы.
Команда doc Если вы знаете имя конкретной функции, вы можете обратиться к её текущей справочной странице напрямую. Например, для получения справочной страницы для функции eval, наберите
doc eval
Команда doc сама запустит ваш Web браузер, если он еще не был запущен ранее.
Печать текущих справочных страниц Версии текущих справочных страниц, как и большинство документации, также доступно в формате PDF (Portable Document Format) через Help Desk. Эти страницы обрабатываются с помощью Adobe's Acrobat reader. Они воспроизводят внешний вид страниц после печати, полностью с шрифтами, графикой, с заданным форматом и рисунками. Это лучший способ получить печатные копии справочных материалов.
Среда MATLAB включает в себя как совокупность переменных, созданных за время сеанса работы MATLAB, так и набор файлов, содержащих программы и данные, которые продолжают существовать между сеансами работы.
Рабочее пространство - это область памяти, доступная из командной строки MATLAB. Две команды, who и whos, показывают текущее содержание рабочего пространства. Команда who выдает краткий список, а команда whos размер и используемую память.
Ниже представлен вывод, осуществленный командой whos, на рабочем пространстве, содержащем результаты из некоторых примеров этой книги. Он показывает различия в структуре данных MATLAB. В качестве упражнения попробуйте найти сегмент кода, который соответствует каждой из ниже приведенных переменных.
whos
Name Size Bytes Class
A 4х4 128 double array D 5х3 120 double array M 10х1 3816 cell array S 1х3 442 struct array h 1х11 22 char array n 1х1 8 double array s 1х5 10 char array v 2х5 20 char array
Grand total is 471 elements using 4566 bytes.
Для удаления всех существующих переменных из рабочего пространства MATLAB, введите
clear
Команда save Команда save сохраняет содержание рабочего пространства в МАТ-файле, который может быть прочитан командой load в последующих сеансах работы MATLAB. Например,
save August17th
сохраняет содержание всего рабочего пространства в файле Augustl7th.mat. Если нужно, вы можете сохранить только определенные переменные, указывая их имена после имени файла. Обычно, переменные сохраняются в двоичном формате, который может быть быстро (и точно) прочитан MATLAB. Если же вы хотите использовать эти файлы вне MATLAB, вы можете указать другой формат.
save August17th -ascii Использует 8-значный текстовой формат.
save August17th -ascii -double Использует 16-значный текстовой формат.
save August17th -ascii -double -tabs Разделяет элементы массива табуляцией.
save August17th -v4 Создает файл для MATLAB 4.
save August17th -append Добавляет данные в существующий МАТ-файл.
Когда вы сохраняете содержание рабочего пространства в текстовом файле, вы должны сохранять только одну переменную в данный момент. Если вы сохраняете более одной переменной, MATLAB создает текстовой файл, но вы не сможете загрузить его обратно.
MATLAB использует маршрут поиска, упорядоченный список директорий, для того, чтобы определить как выполнять функции, которые вы вызываете. Когда вы вызываете стандартную функцию, MATLAB исполняет первый М-файл на своем пути, который имеет заданное имя. Вы можете заменить поведение использованием специальных директорий и поддиректорий.
Команда path показывает маршрут поиска на всех платформах. Выберите опцию Set Path из меню File для просмотра и изменения маршрута.
Команды dir, type, delete и cd осуществляют комплекс групповых операционных системных команд для манипуляций над файлами. Нижеприведенная таблица показывает, как эти команды соответствуют различным операционным системам.
| MATLAB |
MS-DOS |
| dir |
dir |
| type |
type |
| delete |
del erase |
| cd |
chdir |
Для большинства из этих команд вы можете использовать полные пути, шаблоны и указатели дисков в обычной форме.
Команда diary создает дневник сеанса MATLAB в дисковом файле. Вы можете просмотреть и отредактировать конечный текстовой файл, используя любой текстовой процессор. Для создания файла под именем diary, который содержит все команды, которые вы используете, включая вывод на печать (кроме графического вывода), введите
diary
Для сохранения сеанса MATLAB в файле с определенным именем, используйте
diary filename
При остановке записи сеанса работы, наберите
diary off
Запуск внешних программ. Восклицательный знак означает выход из оболочки MATLAB. Он также означает, что последующая строка ввода будет командой к операционной системе. Это очень полезно для вызова утилит или запуска других программ без выхода из MATLAB. Когда вы выходите из внешней программы, операционная система возвращает управление MATLAB.