Равносильные формулы алгебры логики.

Две формулы алгебры логики A и B называются равносильными, если они принимают одинаковые логические значения на любом наборе значений входящих в формулы элементарных высказываний.

Равносильность формул будем обозначать знаком , а запись A B означает, что формулы A и B равносильны.

Например, равносильны формулы: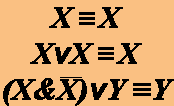

Формула A называется тождественно истинной (или тавтологией), если она принимает значение 1 при всех значениях входящих в нее переменных.

Например, тождественно истинны формулы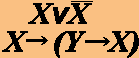

Формула A называется тождественно ложной, если она принимает значение 0 при всех значениях входящих в нее переменных.

Например, тождественно ложна формула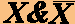

Ясно, что отношение равносильности рефлексивно, симметрично и транзитивно.

Между понятиями равносильности и эквивалентности существует следующая связь: если формулы A и B равносильны, то формула A<=>B – тавтология, то формулы A и B равносильны.

Важнейшие равносильности алгебры логики можно разбить на три группы.

1. Основные равносильности:

2. Равносильности, выражающие одни логические операции через другие: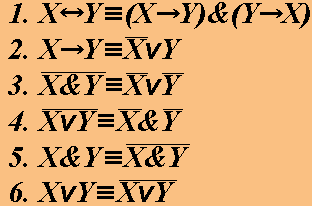

3. Равносильности, выражающие основные законы алгебры логики: