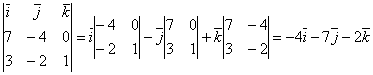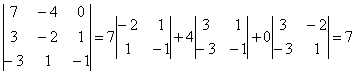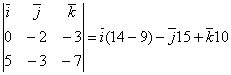Лекция 4.
Скалярное, векторное, смешанное произведение векторов.
Скалярное произведение векторов.
Определение. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Обозначается скалярное произведение символом ( ;
; ) или
) или 
 . Скалярное произведение векторов можно выразить формулами:
. Скалярное произведение векторов можно выразить формулами:

 =I
=I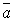 I I
I I I cos(
I cos(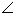 (
(
 ))=I
))=I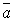 I
I 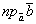 = I
= I I
I 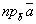 .
.
Отсюда скалярное произведение двух векторов равно произведению длины одного вектора на проекцию на него другого.
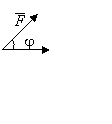
Пусть вектор перемещения 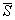 будет неподвижен, а точка приложения вектора силы
будет неподвижен, а точка приложения вектора силы 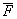 скользит вдоль вектора
скользит вдоль вектора 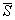 , тогда
, тогда
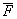
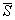 =I
=I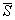 I
I 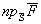 =I
=I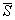 I I
I I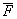 I cosj=A
I cosj=A
есть работа, совершаемая под действием силы 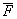 вдоль вектора
вдоль вектора 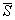 .
.
Скалярное произведение векторов, заданных своими координатами.
Пусть  ={x1, y1, z1} и
={x1, y1, z1} и  ={x2, y2 z2,} тогда
={x2, y2 z2,} тогда 
 = x1 x2+y1 y2+z1 z2 .
= x1 x2+y1 y2+z1 z2 .
Скалярное произведение векторов, заданных своими координатами, равно сумме произведений одноименных координат.
Свойства скалярного произведения.
1) Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда векторы ортогональны: 
 =0
=0 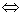 j=
j=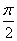 .
.
2) Скалярное произведение коммутативно: 
 =
=
 .
.
3) Ассоциативно относительно скалярного множителя: (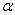
 )
) =
=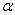 (
(
 ).
).
4) Скалярное произведение дистрибутивно:  (
( +
+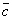 )=(
)=(
 )+(
)+(
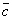 ).
).
5) Свойство скалярного квадрата:  2=I
2=I I2 отсюда I
I2 отсюда I I=
I=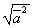 .
.
Рассмотрим таблицу скалярного умножения ортов:
(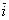 ;
;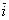 )=(
)=(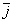 ;
;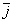 )=(
)=(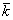 ;
;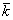 )=1, (
)=1, (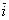 ;
;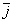 )=(
)=(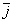 ;
;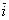 )=(
)=(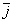 ;
;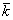 )=(
)=(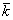 ;
;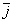 )=(
)=(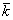 ;
;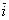 )=(
)=(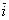 ;
;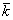 )=0.
)=0.
Скалярное произведение одноименных ортов равно единице, а разноименных - нулю.
Угол между двумя векторами. Из определения скалярного произведения:
cosj=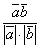 =
=
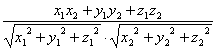 .
.
Условие ортогональности двух векторов:
x1 x2+y1 y2+z1 z2=0.
Условие коллинеарности двух векторов: 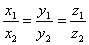 .
.
Проекция вектора на вектор:
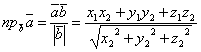 .
.
Векторное произведение.
Определение. Векторным произведением вектора  на вектор
на вектор  называется вектор
называется вектор 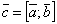 , или
, или 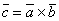 , определяемый следующими тремя условиями:
, определяемый следующими тремя условиями:
1) Модуль вектора  равен
равен 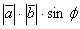 , где
, где 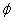 - угол между векторами
- угол между векторами  и
и , т.е.
, т.е.
l l=
l= 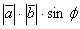 .
.
Отсюда следует, что модуль векторного произведения численно равен площади параллелограмма, построенного на векторах  и
и как на сторонах .
как на сторонах .
2) Вектор  перпендикулярен к каждому из векторов
перпендикулярен к каждому из векторов  и
и (
( ^
^ ;
; ^
^ ), т.е. перпендикулярен плоскости параллелограмма, построенного на векторах
), т.е. перпендикулярен плоскости параллелограмма, построенного на векторах  и
и .
.
3) Вектор  направлен так, что если смотреть из его конца, кратчайший поворот от вектора
направлен так, что если смотреть из его конца, кратчайший поворот от вектора  к вектору
к вектору  был бы против часовой стрелки. (векторы
был бы против часовой стрелки. (векторы  ,
,  ,
,  образуют правую тройку).
образуют правую тройку).
Векторное произведение двух векторов, заданных своими проекциями.
Пусть даны векторы  =x1
=x1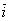 +y1
+y1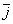 +z1
+z1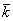 и
и  = x2
= x2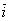 +y2
+y2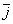 +z2
+z2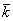 , тогда
, тогда
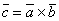 =
=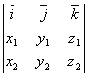 . Если разложить определитель по элементам первой строки, то
. Если разложить определитель по элементам первой строки, то
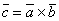 =
=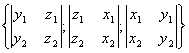 .
.
Механический смысл векторного произведения.
Пусть в точке А к диску приложена сила 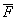 . Определить момент силы
. Определить момент силы 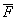 относительно точки О на диске -
относительно точки О на диске - 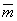 =mom0
=mom0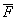 .
.

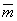 ^
^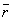 и
и 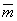 ^
^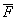 и
и 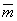 ^(a), l
^(a), l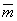 l=l
l=l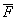 lp=l
lp=l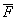 ll
ll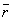 lsin(p-f)=l
lsin(p-f)=l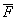 ll
ll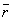 lsin(f).
lsin(f).
Отсюда следует, что 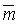 =
=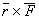
Свойства векторного произведения векторов.
1) Векторное произведение коллинеарных векторов равно нулю.
 ll
ll ( l
( l l¹0; l
l¹0; l l¹0)
l¹0) 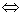
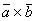 =0.
=0.
2) Антикоммутативность: 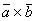 = -
= -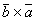 .
.
3) Ассоциативность относительно скалярного множителя: (a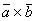 )=a(
)=a(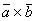 ).
).
4) Дистрибутивность: 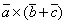 =
= 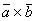 +
+ 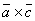 .
.
Таблица векторного умножения ортонормированного базиса 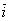 ,
, 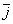 ,
, 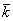 .
.
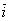 ´
´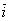 =
=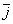 ´
´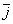 =
=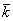 ´
´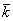 =0,
=0, 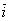 ´
´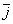 =
=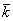 ,
, 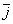 ´
´ 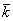 =
=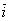 ,
, 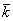 ´
´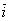 =
=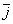 ,
, 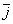 ´
´ 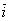 = -
= -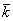 ,
, 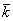 ´
´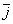 = -
= -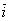 ,
, 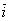 ´
´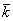 = -
= -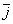 .
.
Для запоминания можно воспользоваться круговым правилом:

Смешанное произведение трех векторов.
Определение. Смешанным произведением трех векторов  ,
,  ,
,  называется векторное произведение двух векторов
называется векторное произведение двух векторов  ´
´ , скалярно умноженное на третий вектор
, скалярно умноженное на третий вектор  : ((
: ((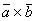 )
) )=(
)=( ,
,  ,
,  )
)
Смешанное произведение есть скалярная величина, по модулю численно равная объему параллелепипеда, построенного на этих векторах как на сторонах.
Пусть 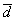 =
=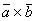 , тогда m=(
, тогда m=( ,
,  ,
,  )=
)=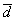
 =l
=l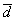 l
l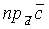 = S
= S (
(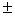 H)=
H)=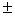 Vпар-да, где “+” означает, что
Vпар-да, где “+” означает, что  ,
, ,
, образуют правую тройку, а “-“ –левую тройку. Отсюда получаем, что
образуют правую тройку, а “-“ –левую тройку. Отсюда получаем, что
Vп-да=l( ,
, ,
, )l; Vтет-да=
)l; Vтет-да=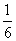 l(
l( ,
, ,
, )l.
)l.
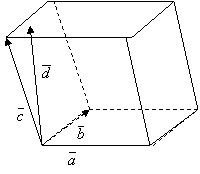
Смешанное произведение векторов, заданных своими координатами.
Если перемножаемые векторы заданы их разложением по ортам:
 =x1
=x1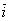 +y1
+y1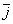 +z1
+z1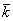 ,
,  = x2
= x2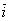 +y2
+y2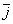 +z2
+z2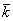 ,
,  =x3
=x3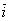 +y3
+y3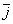 +z3
+z3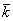 ,
,
то их смешанное произведение будет равно определителю третьего порядка:
( ,
, ,
, )=
)=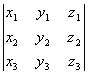 .
.
Свойства смешанного произведения.
1) Если в смешанном произведении перемножаемые векторы переставить в круговом порядке, то произведение не изменится: (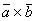 )
) =(
=( ´
´ )
) =(
=( ´
´ )
) .
.
2) Если в смешанном произведении поменять местами знаки векторного и скалярного умножения, то произведение не изменится: (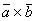 )
) =
= (
( ´
´ ).
).
Это свойство позволяет записывать смешанное произведение в виде ( ,
, ,
, ) без знаков векторного и скалярного умножения.
) без знаков векторного и скалярного умножения.
3) Перестановка в смешанном произведении любых двух векторов изменит лишь его знак: 

 = -
= -

 ;
; 

 = -
= -

 ;
; 

 = -
= -

 .
.
4) Смешанное произведение обращается в нуль, если:
a) хотя бы один из перемножаемых векторов есть нуль- вектор;
b) два из перемножаемых векторов коллинеарные;
c) три перемножаемые вектора компланарны;
Заметим, что случай с) содержит в себе и оба предыдущих: Если хотя бы один из трех векторов есть нуль-вектор или два из них коллинеарны, то все три вектора будут компланарны, следовательно,
 ,
, ,
, -компланарны.Û (
-компланарны.Û ( ,
, ,
, )=0 или
)=0 или 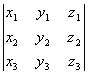 =0.
=0.
Задачи на тему “Векторная алгебра”.
Задача 1. Дано: точки А(-3 1 2 ), В(4 –3 2 ), С(0 –1 3 ), D(-6 2 1 )
Найти: 1) координаты и длину вектора 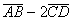 ;
;
2) направляющие косинусы вектора 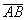 ;
;
3) скалярное произведение 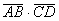 ;
;
4) проекцию пр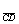
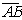 .
.
5) угол между векторами 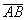 и
и 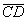 ;
;
6) векторное произведение 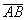 ´
´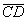 и его модуль;
и его модуль;
7) площадь треугольника АВC;
8) лежат ли точки А,В,С,D в одной плоскости;
9) объем пирамиды АВСD;

 1) Найдем координаты векторов
1) Найдем координаты векторов 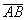 и
и 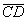 :
:
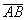 ={4-(-3); -3-2; 2-2},
={4-(-3); -3-2; 2-2}, 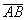 ={7; –4; 0},
={7; –4; 0}, 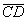 ={-6-0; 2-(-1); 1-3},
={-6-0; 2-(-1); 1-3}, 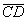 ={-6; 3; –2}.
={-6; 3; –2}.
По правилам действий с векторами, получим
2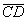 ={-12; 6; –4} и
={-12; 6; –4} и 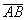 -2
-2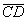 ={7; –4; 0} - {-12; 6; –4} = {19; –10; 4}.
={7; –4; 0} - {-12; 6; –4} = {19; –10; 4}.
Теперь находим длину искомого вектора:
ç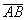 -2
-2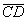 ç=
ç=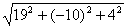 =
=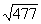 .
.
2) Так как 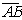 ={7;–4; 0 }, ê
={7;–4; 0 }, ê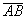 ê=
ê=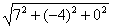 =
=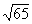 , то направляющие косинусы находятся согласно формулам:
, то направляющие косинусы находятся согласно формулам:
cos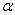 =
=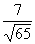 , cosb=
, cosb=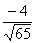 , cos
, cos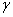 =0.
=0.
3)  (
(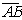 ;
;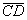 ) найдем по формуле скалярного произведения векторов, заданных своими координатами. Поскольку
) найдем по формуле скалярного произведения векторов, заданных своими координатами. Поскольку 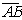 ={7; –4; 0 },
={7; –4; 0 }, 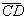 ={-6; 3; –2}, то
={-6; 3; –2}, то
 (
(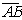 ;
;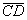 )=7×(-6)+(-4) 3+0×(-2)=-54.
)=7×(-6)+(-4) 3+0×(-2)=-54.
4) На основании формулы проекции, имеем
пр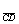
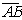 =
=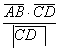 . Отсюда, пр
. Отсюда, пр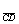
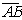 =
=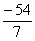 .
.
5) Заметим, что вектора 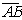 ={7 –4 0 } и
={7 –4 0 } и 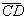 ={-6 3 –2} не являются коллинеарными, поскольку не пропорциональны их координаты:
={-6 3 –2} не являются коллинеарными, поскольку не пропорциональны их координаты:
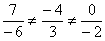 .
.
Эти вектора не являются также перпендикулярными, так как их скалярное произведение  (
(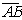 ;
; 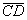 )
)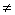 0.
0.
Угол 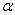 =
= Ð(
Ð(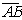 ;
;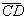 ) найдем из формулы:
) найдем из формулы:
cos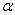 =
=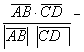 .
.
Ранее было найдено (
(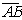
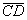 ) = - 54,
) = - 54, 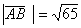 ,
, 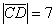 , стало быть,
, стало быть,
cos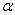 =
=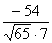 .
.
6) По формуле векторного произведения, имеем
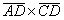 =
=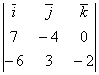 =
=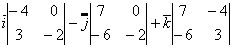 =8
=8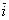 +14
+14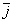 -3
-3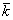 .
.
Таким образом, векторное произведение имеет координаты:
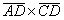 ={8; 14; –3}, а его модуль
={8; 14; –3}, а его модуль 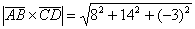 =
=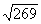 .
.
7) Применив формулу площади для треугольника ABC, построенного на векторах
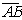 ,
, 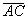 , получаем
, получаем 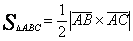
 .
.
Векторное произведение 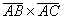 и его модуль найдем, аналогично решению задачи 6):
и его модуль найдем, аналогично решению задачи 6):
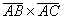 =
=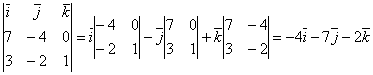 ,
,
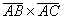 ={-4; –7; –2},
={-4; –7; –2}, 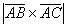 =
=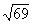 .
.
Отсюда получаем, что 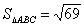 (кв. ед.)
(кв. ед.)
8) Точки A,B,C,D будут лежать в одной плоскости, если три вектора, соединяющие эти точки, являются компланарными. Составим, например, вектора 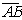 ={7; –4; 0},
={7; –4; 0},
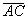 ={3; –2; 1},
={3; –2; 1}, 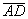 ={-3; 1; –1} и найдем их смешанное произведение:
={-3; 1; –1} и найдем их смешанное произведение:
(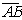 ;
;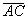 ;
;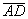 )=
)=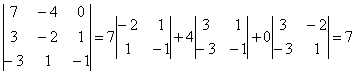 ,
,
Поскольку (
(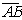 ;
;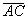 ;
;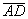 )
)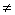 0, то вектора
0, то вектора 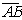 ,
,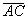 ,
,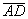 не компланарны, а стало быть, точки A,B,C,D не лежат в одной плоскости.
не компланарны, а стало быть, точки A,B,C,D не лежат в одной плоскости.
9) Так как объем пирамиды равен 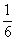 части объема параллелепипеда, построенного на векторах
части объема параллелепипеда, построенного на векторах 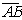 ,
, 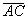 ,
, 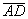 вычисляется по формуле
вычисляется по формуле
 Vпир=
Vпир=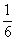 Vпар-да=
Vпар-да=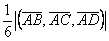 , то используя решение задачи 8), получим Vпир=
, то используя решение задачи 8), получим Vпир=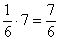 (куб.ед.) .Ñ
(куб.ед.) .Ñ
Задача 2. Определить при каких 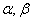 вектора
вектора 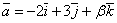 и
и 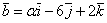 коллинеарны.
коллинеарны.
D В случае коллинеарности, соответствующие координаты векторов ={-2;3;
={-2;3;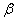 } и
} и  ={
={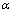 ; -6; 2} должны быть пропорциональны, то есть:
; -6; 2} должны быть пропорциональны, то есть: 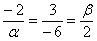 .
.
Отсюда 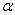 =4 и
=4 и 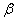 =-1Ñ
=-1Ñ
Задача 3. Определить при каком 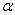 вектора
вектора 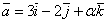 и
и 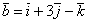 перпендикулярны.
перпендикулярны.
D Вектора 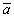 ={3;–2;
={3;–2;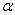 } и
} и  ={1;3;-1} перпендикулярны, если их скалярное произведение
={1;3;-1} перпендикулярны, если их скалярное произведение 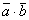 равно нулю. Из этого условия получаем:
равно нулю. Из этого условия получаем: 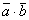 =
=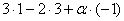 =0. Стало быть,
=0. Стало быть, 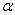 =-3. Ñ
=-3. Ñ
Задача 4. Вычислить, какую работу производит сила 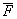 {-5 2 1}, когда точка ее приложения перемещается из A(3; 0; 3) в B(-4; 1; 2).
{-5 2 1}, когда точка ее приложения перемещается из A(3; 0; 3) в B(-4; 1; 2).
Образуем вектор перемещения 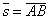 ={-7; 1; -1}.
={-7; 1; -1}.
Тогда работа A=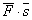 = 36. Ñ
= 36. Ñ
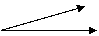
Задача 5. Найти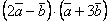 , если
, если  =1,
=1, 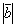 =3,
=3, 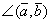 =
=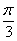 .
.
D В силу свойств скалярного произведения, имеем:
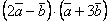 =2
=2
 +6
+6
 -
-
 -3
-3
 =2
=2 2+5
2+5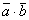 -3
-3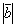 2=2
2=2 2+5
2+5
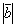 cos
cos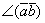 --3
--3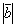 2.
2.
Подставляя теперь в правую часть данные задачи, получим 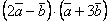 = -17,5.Ñ
= -17,5.Ñ
Задача 6. Сила 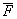 {5;–3; -7} приложена в точке В(2;1;1). Определить момент силы относительно точки К(2; 3; 4).
{5;–3; -7} приложена в точке В(2;1;1). Определить момент силы относительно точки К(2; 3; 4).
D Образуем вектор 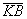 ={0 –2 -3}. Тогда момент относительно точки К вычисляется по формуле:
={0 –2 -3}. Тогда момент относительно точки К вычисляется по формуле: 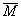 =momK
=momK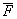 =
=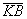
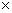
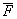 .
.
Имеем,
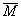 =
=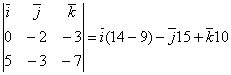 , или
, или 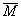 ={5; –15; 10}. Ñ
={5; –15; 10}. Ñ
Задача 7. Найти 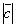 , если
, если 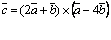 ,
,  =1,
=1, 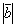 =3,
=3, 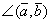 =
=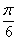 .
.
D Используя свойства векторного произведения, упростим конструкцию вектора 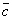 , а именно:
, а именно:
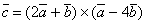 =2
=2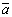
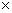
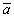 - 8
- 8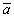
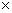
 +
+
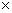
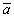 - 4
- 4
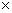
 .
.
Так как 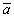 II
II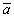 ,
,  II
II , то
, то 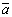
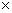
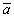 =
=
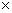
 =0. Следовательно,
=0. Следовательно,
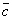 = - 8
= - 8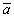
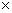
 +
+
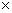
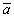 = - 9
= - 9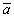
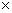
 .
.
Теперь по формуле модуля векторного произведения, получаем
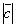 =I - 9
=I - 9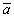
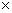
 I=9I
I=9I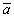
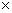
 I=9
I=9
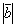 sin
sin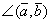 =27 sin
=27 sin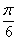 =13,5. Ñ
=13,5. Ñ
![]() ;
;![]() ) или
) или ![]()
![]() . Скалярное произведение векторов можно выразить формулами:
. Скалярное произведение векторов можно выразить формулами:![]()
![]() =I
=I![]() I I
I I![]() I cos(
I cos(![]() (
(![]()
![]() ))=I
))=I![]() I
I ![]() = I
= I![]() I
I ![]() .
.
![]() будет неподвижен, а точка приложения вектора силы
будет неподвижен, а точка приложения вектора силы ![]() скользит вдоль вектора
скользит вдоль вектора ![]() , тогда
, тогда ![]()
![]() =I
=I![]() I
I ![]() =I
=I![]() I I
I I![]() I cosj=A
I cosj=A![]() вдоль вектора
вдоль вектора ![]() .
.![]() ={x1, y1, z1} и
={x1, y1, z1} и ![]() ={x2, y2 z2,} тогда
={x2, y2 z2,} тогда ![]()
![]() = x1 x2+y1 y2+z1 z2 .
= x1 x2+y1 y2+z1 z2 .![]()
![]() =0
=0 ![]() j=
j=![]() .
.![]()
![]() =
=![]()
![]() .
.![]()
![]() )
)![]() =
=![]() (
(![]()
![]() ).
).![]() (
(![]() +
+![]() )=(
)=(![]()
![]() )+(
)+(![]()
![]() ).
).![]() 2=I
2=I![]() I2 отсюда I
I2 отсюда I![]() I=
I=![]() .
.![]() ;
;![]() )=(
)=(![]() ;
;![]() )=(
)=(![]() ;
;![]() )=1, (
)=1, (![]() ;
;![]() )=(
)=(![]() ;
;![]() )=(
)=(![]() ;
;![]() )=(
)=(![]() ;
;![]() )=(
)=(![]() ;
;![]() )=(
)=(![]() ;
;![]() )=0.
)=0.![]() =
=![]()
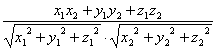 .
.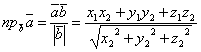
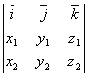 . Если разложить определитель по элементам первой строки, то
. Если разложить определитель по элементам первой строки, то 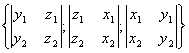 .
.


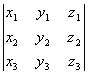
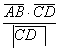
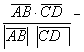
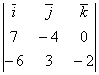 =
=