Лекция 3.

Векторная алгебра.

Величины бывают скалярные и векторные. Скалярной величиной или скаляром называется величина, которая вполне определяется своим численным значением.

Примеры физических скалярных величин: t-температура; m-масса; r-плотность распределения массы; L- длина; S-площадь и т.д.

Вектором или векторной величиной называется величина, которая характеризуется не только своим численным значением, но и определенным направлением в рассматриваемом пространстве.

 Векторы- сила, скорость, ускорение, напряженность электрического поля .

Определение. Направленный отрезок (или, и что то же, упорядоченная пара точек - начало и конец отрезка) будем называть вектором.

Геометрическое изображение вектора:

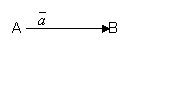
Обозначение вектора: , либо  . Направление на отрезке обозначается  стрелкой.

Расстояние между началом и концом  вектора называется его модулем или абсолютной величиной  и обозначается: ll, ll.

Нулевой вектор- вектор, у которого начало и конец совпадают. Он обозначается  и его модуль равен нулю, а направление неопределенное.

Определение.  Векторы называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. Обозначают: ll.

Определение. Векторы называются компланарными, если существует плоскость, которой они параллельны.

В учебном пособии рассматриваются свободные векторы, то есть равенство двух векторов понимается  следующим образом:

Определение. Два вектора называются равными, если они коллинеарные, одинаково направлены и  имеют одинаковую длину.

Из этого определения следует, что  вектор параллельно самому себе, не изменяя направления, можно переносить в любую точку пространства.

Векторы являются предметом векторного исчисления подобно тому, как числа являются предметом арифметики .

Линейные операции над векторами.

К линейным операциям над векторами относятся операции умножения вектора на число и сложение векторов.

Определение.  Под произведением вектора   на число a понимается вектор , удовлетворяющий следующим условиям:

1)      ll=lal ll;

2)       вектор  коллинеарен вектору  (ll  );

3)       векторы и  направлены одинаково, если a>0 и противоположно, если a <0.

Произведение вектора  на число a обозначается a.

Замечание 1.  Пусть a= ( ll¹0 ), рассмотрим вектор =, тогда ll==1. Векторы  и  коллинеарны и одинаково направлены, тогда -единичный вектор, сонаправленный с . Вектор - орт вектора  , и обозначается ⁰, т.е. =⁰ и =ll или =⁰ ll.

Замечание 2. Пусть дан вектор ¹0. Для любого коллинеарного ему вектора  существует и притом одно число l, удовлетворяющее равенству =l. Тогда ll=IlI ll и l=, если и одинаково направлены и  l= -, если они противоположно направлены.

Определение. Суммой двух векторов  и  с общим началом,  является диагональ параллелограмма (), построенного на этих векторах  как на сторонах 
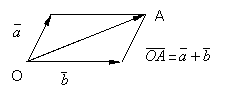
( правило параллелограмма ).Правило треугольника: начало следующего вектора поместить в конец предыдущего и вектор, соединяющий начало первого с концом последнего есть вектор суммы.

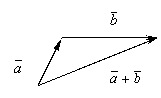Чтобы сложить несколько векторов, достаточно начало каждого последующего вектора совместить с концом предыдущего, тогда замыкающий вектор, идущий из начала первого в конец последнего, будет вектором суммы (правило многоугольника).

Определение. Вектором, противоположным к данному вектору , называется коллинеарный  вектор -, модуль которого равен модулю вектора , а направление противоположно.

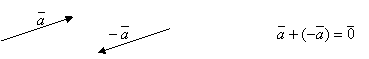
Определение. Под разностью двух векторов  и  понимается такой третий вектор =-, который при сложении с вычитаемым вектором  дает уменьшаемый вектор .

Правило построения разности векторов  и :

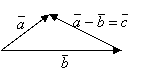Приводим векторы   и  к общему началу, и соединяем концы векторов   и . Вектор разности направлен из конца вычитаемого вектора () в конец уменьшаемого вектора ().

Свойства линейных операций над векторами.

1)         Сложение векторов коммутативно, т.е. для любых векторов  и  выполнено +=+.

2)         Сложение векторов ассоциативно, т.е. для любых векторов, и   выполнено  + (+) = ( + )+.

3)         Прибавление нулевого вектора  к любому вектору ,  не меняет последнего: +=.

4)         Для любого вектора  вектор - является противоположным, т.е. +(-)=.

5)         Умножение вектора на число ассоциативно, т.е. для любых чисел a и b и любого вектора , выполнено (ab)=a(b)=b(a).

6)         Умножение вектора на число дистрибутивно по отношению к сложению чисел: (a+b)=a+b.

7)         Умножение вектора на число дистрибутивно по отношению к сложению векторов: a(+)=a+a.

8)         Умножение вектора на единицу не меняет вектора: 1=.

Понятие линейной зависимости векторов.

Определение. Пусть дана система векторов ₁, ₂, …,_n и совокупность n вещественных чисел a₁, a₂,…,a_n . Тогда выражение вида   a₁₁ +a₂₂ +…+a_nn называется линейной комбинацией векторов, а числа  a₁, a₂,…, a _n   называются коэффициентами линейной комбинации.

Если некоторый вектор  представлен как линейная комбинация векторов₁, ₂, …,_n т.е. в виде:  = a₁₁ +a₂₂ +…+a_nn, то говорят, что вектор  разложен по этим векторам.

Определение. Векторы ₁, ₂, …,_n называются линейно зависимыми, если существует набор коэффициентов a₁, a₂,…,a_n, одновременно не равных нулю

(a²₁+ a²₂,+…+a²_n¹0) и таких, что a₁₁ +a₂₂ +…+a_nn=0.

Определение. Векторы ₁, ₂, …,_n называются линейно независимыми, если равенство нулю линейной комбинации этих векторов возможно лишь при всех коэффициентах одновременно равных нулю.

Определение. Базисом на прямой называется любой ненулевой вектор на этой прямой.

Определение. Базисом на плоскости называются два неколлинеарных вектора на этой плоскости, взятые в определенном порядке.

Определение.  Базисом в пространстве R³ называются три линейно независимые вектора в этом пространстве, взятые в определенном порядке.

Теорема о разложении вектора по базису в пространстве R³.
Пусть даны три некомпланарные вектора ,,. Любой вектор  раскладывается по ним. Такое разложение единственно. Существует набор чисел  a₁, a₂, a₃ такой, что:  = a₁+a₂+a_3.

Свойства линейно зависимой и линейно независимой системы векторов.

1)      Если хотя бы один из n векторов есть нуль вектор, то все n векторов  лин. зависимы.

2)      Если среди n векторов какие-либо n-1 векторов лин. зависимы, то все n векторов лин. зависимы.

3)       Для того чтобы два ненулевых вектора были лин. зависимы необходимо и достаточно, чтобы они были коллинеарными.

4)      Пусть и - два неколлинеарных вектора плоскости. Любой компланарный с ними вектор  раскладывается по ним: =a₁ +a₂ . Такое разложение единственно.

5)      Три компланарных вектора линейно зависимы. Три некомпланарные вектора пространства линейно независимы .

6)      Любые четыре вектора пространства R³ линейно зависимы.

7)      Система векторов ₁, ₂, …,_n линейно зависима тогда и только тогда, когда один из них раскладывается в линейную комбинацию остальных.

Понятие о проекциях.

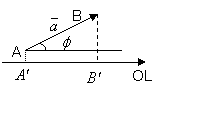
Пусть дан вектор  и ось OL, j- угол между вектором и  положительным направлением оси OL. A’ и B’- основания перпендикуляров, опущенных из точек А и В соответственно

Определение. Проекцией вектора на ось называется длина отрезка оси A^lB^l, взятая со знаком плюс, если вектор  образует острый угол с направлением оси, и со знаком минус в противоположном случае.

Теорема. Проекция вектора  на ось OL равна произведению длины вектора на косинус угла между вектором и осью: =II cosj.

Следствие. При умножении вектора  на некоторое число a его проекция умножается на это же число: = a.

Теорема о проекции суммы. Проекция суммы некоторого числа векторов на ось(L) равна сумме проекций слагаемых векторов: =++, =++.

Декартова система координат.

Точка- начало координат О(0,0,0). Ортонормированный базис образуют  взаимно перпендикулярные векторы ,, единичной длины, т.е. ll=ll=ll=1 и (^)=(^)=(^)=. Прямые, проходящие через начало координат в направлении векторов ,, называются осями координат. Векторы ,, определяют положительное направление осей координат: OX, OY, OZ - оси абсцисс, ординат и аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями OXY, OXZ, OYZ.

Определение. Прямоугольной системой координат в пространстве называется совокупность какой-либо точки (О) и ортонормированного базиса.

Определение. Радиусом-вектором произвольной точки М по отношению к точке О, называется вектор . Точке М можно сопоставить упорядоченную тройку чисел (x,y,z)- компоненты ее радиус-вектора: М(x, y, z) и =={x,y,z}.

Определение. Компоненты радиус-вектора точки М по отношению к началу координат называют координатами точки М в рассматриваемой системе координат.

рис1	рис2

 

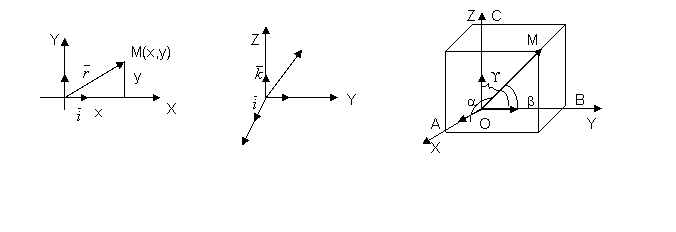
Координаты вектора  совпадают с проекцией вектора на соответствующие оси координат:

  x=, y=, z=,  =x+y+z, ={x,y,z}  (рис. 1).

 Из рис. 2 имеем:  === x+y+z, OA=x, OB=y, OC=z,

   ll==.

 Пусть вектор задан координатами крайних точек =, А(x₁,y₁,z₁)

и В(x₂,y₂,z₂), тогда ==-=x₂+y₂+z₂-(x₁+y₁+z₁) =

=(x₂ -x₁)+(y₂ -y₁)+(z₂ -z₁).

Следовательно, чтобы определить координаты вектора по координатам крайних точек, надо из координат конца вычесть соответствующие координаты начала: ={x₂-x₁, y₂-y₁, z₂-z₁ }.

Определение. Пусть a, b, ¡- углы между вектором  и соответственно ортами ,, (рис. 2), тогда направляющие косинусы вектора определяются по правилу:

соs a==,  соsb==, соs¡==,

Следовательно, сумма квадратов направляющих косинусов равна 1: сos²a+сos²b+сos²¡=1.

Связь компонент, проекций, направляющих косинусов и коэффициентов в разложении по базису.

Пусть вектор ={x, y, z} в пространстве R³; ,,-ортонормированный базис в данной системе координат, a, b, ¡- углы между вектором  и соответственно ортами ,,, тогда

=x+y+z, где x, y, z-составляющие вектора ,

x, y, z- координаты вектора  в базисе ,,,

x==ll сosa, y==ll сosb, z==ll сos¡.

Деление отрезка в данном отношении.

Пусть А(x₁,y_1,z₁), B(x₂,y₂,z₂). Координаты точки С(x,y,z) на отрезке АВ, которая делит этот отрезок в отношении , т.е. , определяются по формулам:

 x=, y=, z=.

Координаты середины отрезка АВ соответствуют значению =1 и определяются как полусумма координат концов отрезка:

x=, y=, z=.

Линейные операции над векторами, заданными своими координатами.

Пусть ={x₁, y₁, z₁} и ={x₂, y₂, z₂}.

1) При умножении вектора на число каждая координата вектора умножается на это число: =a, aÎR, тогда ={ ax₁, ay₁, az₁}.

2) При сложении (вычитании) векторов их одноименные координаты складываются (вычитаются): =+, тогда ={ x₁+x₂, y₁+y₂, z₁+z₂}.

 

На главную

В начало