6.30. Способ 1. (Метод неопределенных коэффициентов).

Составляем таблицу истинности для функции x 1 x 2

Записываем полином Жегалкина с неизвестными коэффициентами a 0, a 1, a 2, a 12 для функции от двух переменных: x 1 x 2 = a 0 Å a 1 x 1 Å a 2 x 2 Å a 12 x 1 x 2 .

Подставляя в это разложение значения x 1 и x 2 из таблицы, определяем неизвестные коэффициенты:

Подставляя x 1=0, x 2=0, получаем: 1= a 0;

x 1 =0, x 2=1 — 0=1 Å a 2 Þ a 2=1;

x 1=1, x 2=0 — 0=1 Å a 1 Þ a 1=1;

x 1=1, x 2=1— 1=1 Å a 12 Þ a 12=0.

Полином Жегалкина имеет вид: x 1~x 2 = 1 Å x 1 Å x 2 .

Способ 2. (Эквивалентные преобразования).

Сначала запишем СДНФ эквивалентности:

{т.к. } = {поскольку } {далее, , поэтому }

7.30. Сначала преобразуем исходную формулу: ; . . Пусть , тогда , , поэтому , следовательно функция несамодвойственна.

8.30. Функция немонотонная, т.к. , но .

9.30. Для доказательства полноты системы необходимо проверить, что система содержит функцию не сохраняющую 0, функцию не сохраняющую 1, немонотонную функцию, несамодвойственную функцию и нелинейную функцию. Докажем полноту системы . Обозначим и выпишем ее таблицу истинности

Функция f 1 не сохраняет 0. Выясним, является ли f 1 самодвойственной.

Т.к. , то f 1 несамодвойственна.

Функция немонотонная, и не сохраняет 1. Найдем полином Жегалкина для =

; ; ; ;

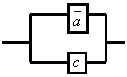
Функция нелинейная. Согласно теореме о полноте – полная система.

10.20. Составим функцию проводимости для схемы:

Полученной формуле соответствует схема: