1.30. Составим таблицу истинности для формулы 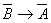 : :
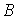
|
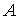
|
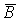
|
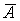
|
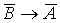
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
2.30. Проверим эквивалентность формул 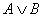 и и 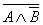 , составив для них таблицы истинности. , составив для них таблицы истинности.
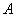
|
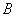
|
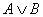
|
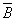
|
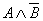
|
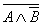
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
Формулы не эквивалентны, так как 3-й и 6-й столбцы таблицы не совпадают.
3.30. Для упрощения формулы используем правило исключения импликации: 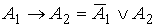 . .
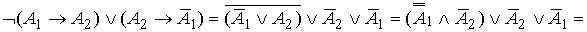
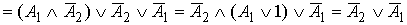 . .
4.30. Используя законы логики приведем формулу 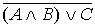 к виду, содержащему только дизъюнкции элементарных конъюнкций. Полученная формула и будет искомой ДНФ: к виду, содержащему только дизъюнкции элементарных конъюнкций. Полученная формула и будет искомой ДНФ:
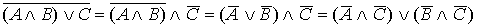
Для построения СДНФ составим таблицу истинности для данной формулы:
A |
B |
C |
A Ù B |
(A Ù B ) Ú C |
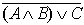
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
Помечаем те строки таблицы, в которых формула (последний столбец) принимает значение “1”. Для каждой такой строки выпишем формулу, истинную на наборе переменных A,B,C данной строки: строка 1 – 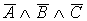 ; строка 3 – ; строка 3 – 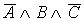 ; строка 5 – ; строка 5 – 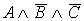 . Дизъюнкция этих трех формул будет принимать значение “1” только на наборах переменных в строках 1, 3, 5, а следовательно и будет искомой совершенной дизьюнктивной нормальной формой (СДНФ): . Дизъюнкция этих трех формул будет принимать значение “1” только на наборах переменных в строках 1, 3, 5, а следовательно и будет искомой совершенной дизьюнктивной нормальной формой (СДНФ): 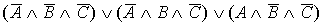
5.30. Для того, чтобы записать формулу в приведенном виде, следует , пользуясь формулой 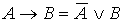 , исключить операцию импликации, а затем “опустить” операцию отрицания на простые переменные: , исключить операцию импликации, а затем “опустить” операцию отрицания на простые переменные: 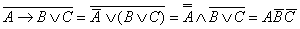 . .
|