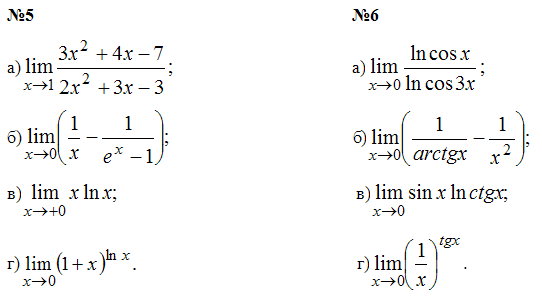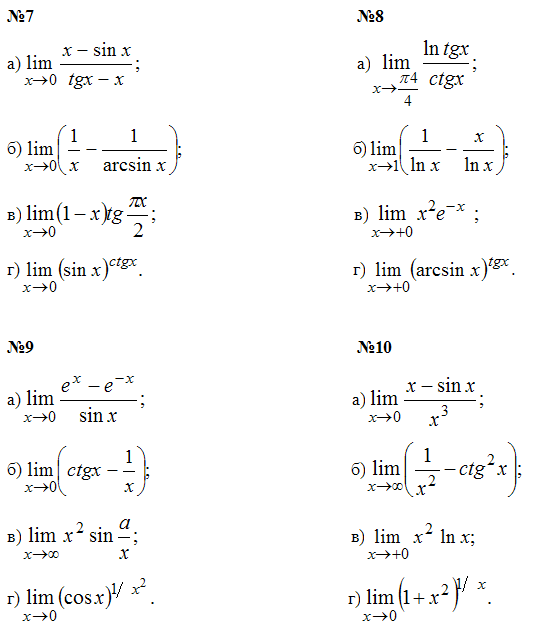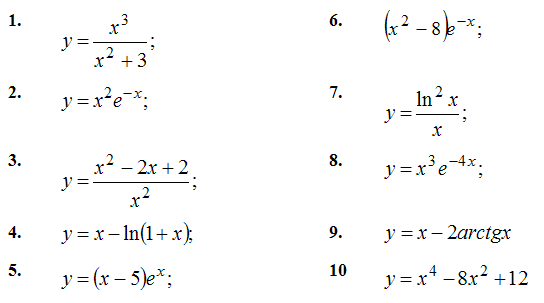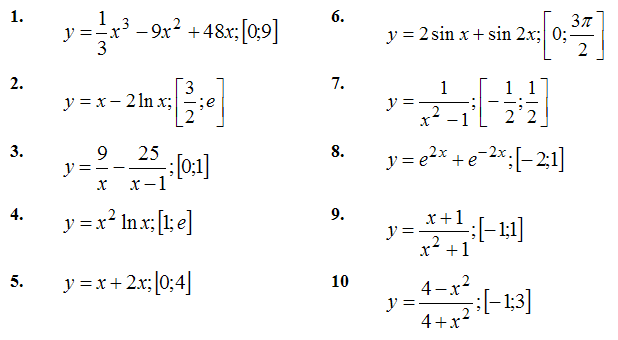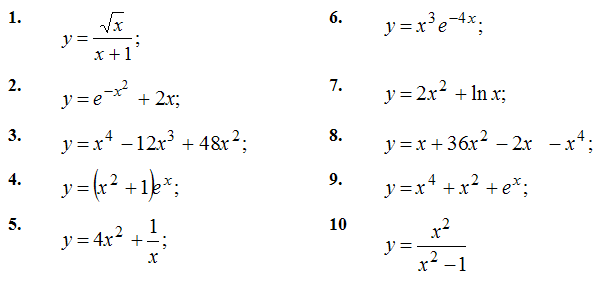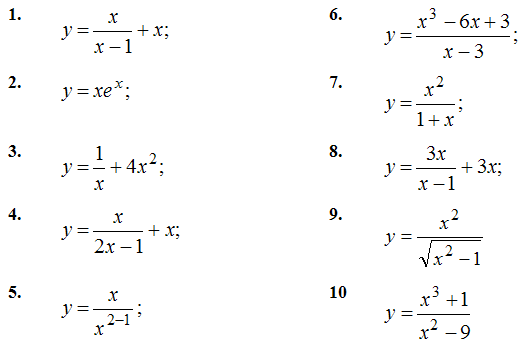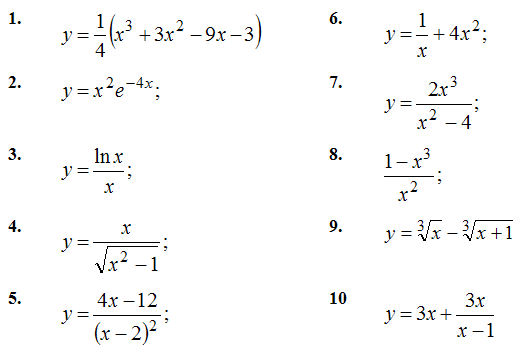Контрольная работа №4

Задача №1. Составить уравнение касательной и нормали к кривой у = f(x) в точке:

1) к кривой  в точке М(2;4);

2) к параболе  при х = -0,5;

3) к кривой в точке М(2;12);

4) к кривой  в точке М(-2;5);

5) к кривой y = t cost; y = t sint в точке ;

6) к кривой  в точках пересечения с прямой у = 1;

7) к кривой  в точке пересечения с осью Ох;

8) к циклоиде  в точке, для которой

9) к астроиде  в точке, для которой

10) к кривой  в точке, для которой

Задача №2. Найти пределы функций, используя правило Лопиталя: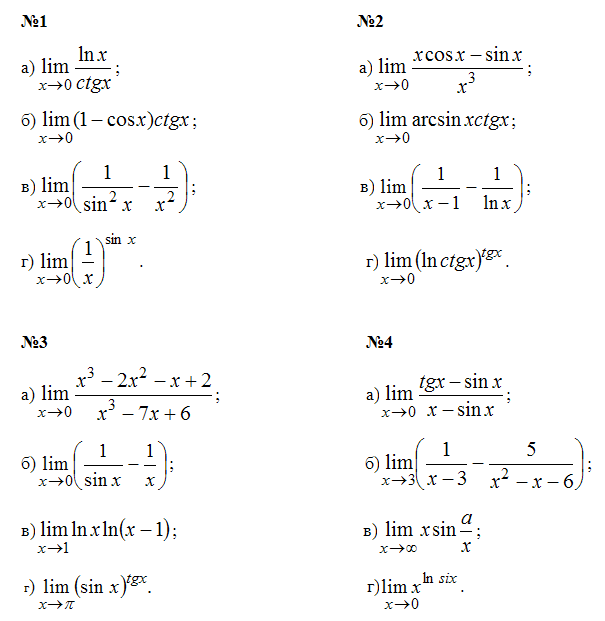

Задача №3. Найти экстремум функции:

Задача №4. Найти наибольшее и наименьшее значение функции y = f(x) на отрезке (a; b):

Задача №5. О наибольших и наименьших значениях величин:

1.Найти такое положительное число, чтобы разность между ним и его кубом была наибольшей.

2. В данный шар вписать конус наибольшего объёма.

3. Каковы должны быть размеры консервной банки, имеющей наибольший объём при заданной площади поверхности?

4. Найти радиус основания цилиндра наибольшего объёма, который можно вписать в шар радиуса R.

5. Вычислить наибольший объём цилиндра, полная поверхность которого равна S.

6. Из круглого листа жести вырезают сектор и свёртывают его в коническую воронку. Каким должен быть угол сектора, чтобы воронка имела наибольший объём?

7. Число 180 разбить на 3 слагаемых так, чтобы 2 из них относились как 1:2, а произведение всех трёх слагаемых было бы наибольшим.

8. Из круглого листа вырезать такой сектор, чтобы, свернув его, получить воронку наибольшей вместимости.

9. Открытый жестяной бак с квадратным основанием должен вмещать V литров. При каких размерах на изготовление бака потребуется наименьшее количество жести?

10. Найти высоту цилиндра наибольшего объема, который можно вписать в шар радиуса R.

Задача №6. Найти интервалы выпуклости, вогнутости графика функции и точки перегиба:

Задача №7. Найти асимптоты кривой:

Задача №8. Провести полное исследование функции и построить график: