5. Примеры.
Проверить сходимость последовательности xn в метрических пространствах s, lp(p³1) или m.
Указание 1. Если существует предел xn по метрике, то он равен покоординатному пределу.
1.Проверить сходимость последовательности xn в пространствах
s и m, если xn,k=1 при k=n и xn,k=0 при k¹n.
Решение.
x1={1,0,0,0,…},
x2={0,1,0,0,…},
x3={0,0,1,0,…},…
Покоординатный предел существует и равен q={0,0,0,0,…}. Поскольку покоординатная сходимость равносильна сходимости по метрике s, то xn®q в s.
Однако в пространстве m limn®¥r(xn,q)= limn®¥1=1¹0, поэтому q не является пределом xn по метрике пространства m. А тогда у xn
Вообще не может быть предела в m, то есть последовательность
xn не является сходящейся в m.
2.Проверить сходимость последовательности xn в пространствах
s и m, если xn,k=(k+n)/n.
Решение.
Предел по каждой координате равен limn®¥ xn,k= limn®¥(k+n)/n= limn®¥(k/n+1)=1, поэтому в s имеет место сходимость xn®e={1,1,1,1,…}. О сходимости в m говорить не имеет смысла вообще, поскольку xnÏm. Действительно, при любом фиксированном n limk®¥(k+n)/n=¥, поэтому supk| xn,k |=¥.
3.Проверить сходимость последовательности xn в пространствах
lp(p³1) и m, если xn,k=1/(nk).
Решение.
Рассмотрим числовой ряд åk=1¥| xn,k |p=åk=1¥1/(npkp). При любом фиксированном n этот ряд сходится для p>1 (и тогда xnÎ lp) и расходится для p=1 (тогда xnÏ lp, говорить о сходимости не имеет смысла).
Поскольку для всякого фиксированного k мы имеем limn®¥ xn,k= limn®¥1/(nk)=0, то у последовательности xn существует покоординатный предел q={0,0,0,0,…}Îlp. Если p>1, то ряд åk=1¥1/kpсходится, и тогда в пространстве lp
limn®¥r(xn,q)=limn®¥(åk=1¥1/|nk|p)1/p=
=limn®¥(åk=1¥1/(npkp))1/p= limn®¥1/n(åk=1¥1/(kp))1/p=0,
поэтому xn®q в lp (p>1). Поскольку сходимость в любом lp сильнее, чем в m, то и в пространстве m имеет место сходимость xn®q.
4.Проверить сходимость последовательности xn в пространствах
lp(p³1) и m, если xn,k=1/(k(nk)1/2).
Решение.
Числовой ряд åk=1¥|xn,k| =åk=1¥1/(n1/2k3/2) сходится, поскольку 1,5>1, следовательно, все xnÎ l1Ì lpÌ m. У последовательности xn, очевидно, существует покоординатный предел q={0,0,0,0,…}, и в пространстве l1
limn®¥r(xn,q)= limn®¥åk=1¥|xn,k|= limn®¥1/n1/2åk=1¥1/k3/2=0.
Таким образом, xn®q в l1. Сходимость в l1 сильнее, чем в остальных
lp(p>1) и в m, поэтому xn®q во всех пространствах m и lp(p³1).
5.Проверить сходимость последовательности xn в пространстве
m, если xn,k=(k+n)/(3+k+n).
Решение.
Поскольку "k,n(ÎN) 0< xn,k<1, то все xnÎm. При любом фиксированном k limn®¥xn,k= limn®¥(k/n+1)/((3+k)/n+1)=1,
Поэтому у последовательности существует покоординатный предел e={1,1,1,1,…}. В пространстве m
limn®¥r(xn,e)=limn®¥supk|xn,k|=limn®¥supk|(k+n)/(3+k+n)-1|= limn®¥supk3/(3+k+n)= limn®¥3/(4+n)=0.
Итак, xn®q по метрике пространства m.
6.Проверить сходимость последовательности xn в пространстве
m, если xn,k=(n)/(k+2n).
Решение.
Так как 0< xn,k<1/2, то все xnÎm. Найдем покоординатный предел:
y={1/2,1/2,1/2,1/2,…}Îm.
Замечание. Если последовательность xn сходится в m, то ее пределом может быть только y (см. указание 1).
Оценим метрику r(xn,y):
r(xn,y)= supk|xn,k-1/2|= supk k/(2(k+2n))³ n/(2(n+2n))=1/6.
Поскольку r(xn,y) ³ 1/6, то limn®¥r(xn,y)¹0. Вывод: y не является пределом xn, и, согласно замечанию, последовательность xn не является сходящейся в m.
7.Проверить сходимость последовательности xn в пространствах
lp(p³1) и m, если xn,k=1/(2n+k).
Решение.
Числовой ряд åk=1¥|xn,k|p =åk=1¥1/(2n+k)p~åk=1¥1/kp сходится при p>1 и расходится при p=1 (нет смысла говорить о сходимости в l1последовательности xn Ïl1). Таким образом, xn Î lpÌ m (p>1). Покоординатным пределом xn является q={0,0,0,0,…}. Вычислим метрику r(xn, q) в lp (p>1):
r(xn, q)=(åk=1¥|xn,k|p)1/p=(åk=1¥1/(2n+k)p)1/p.
Обозначив m =2n+k, получаем r(xn,q)=(åm=2n+1¥1/mp)1/p.
Величина åm=2n+1¥1/mp является остатком сходящегося ряда åm=1¥1/mp и поэтому стремится к 0, когда n®¥. А тогда limn®¥r(xn, q)=0, что означает сходимость xn к q в lp (p>1). Из сходимости в lp (p>1) следует, что и в m xn® q.
8.Проверить сходимость последовательности xn в пространстве
m, если xn,k=1/n+1/k.
Решение.
Так как, 0<xn,k<2, то xnÎm. Пределы координат: yk=limn®¥xn,k=1/k.
Так как 0<yk<1, то покоординатный предел y={1/,1/2,1/3,1/4,…}Îm. По метрике пространства m
r(xn,y)= supk|xn,k-yk|= supk 1/n=1/n®0 при n®¥. Таким образом, xn® y в m.
9.Проверить сходимость последовательности xn в пространстве
m, если xn,k=n/(n2+k).
Решение.
Так как, 0<xn,k<n/n2=1, то xnÎm. Поскольку limn®¥xn,k= limn®¥(1/n)/(1+k/n2)=0, то у xn существует покоординатный предел q={0,0,0,0,…} Îm. Оценим метрику r(xn, q):
0£r(xn,q)=supkn/(n2+k)=n/(n2+1)<1/n. Так как 1/n®0 при n®¥, то и limn®¥r(xn, q)=0, то есть xn® q в m.
10.Проверить сходимость последовательности xn в пространстве l1, если xn,k=n/(nk2+1).
Решение.
Числовой ряд åk=1¥|xn,k|=åk=1¥1/(k2+1/n)~åk=1¥1/k2 сходится (т.к. показатель степени 2>1), т.е. xnÎl1. Пределы координат:
yk=limn®¥xn,k= limn®¥1/(k2+1/n)=1/k2,
а это значит, что у xn есть покоординатный предел: y={1/,1/4,1/9,…}. При этом yÎl1. Оценим метрику r(xn,y) в пространстве l1:
0£r(xn,y)=åk=1¥|xn,k-yk|=åk=1¥|n/(nk2+1)-1/k2|=
=åk=1¥ 1/((nk2+1) k2)<åk=1¥ 1/(nk2)=1/nåk=1¥ 1/k2.
Тогда limn®¥r(xn,y)=0, т.е. xn® y по метрике l1.
11.Проверить сходимость последовательности xn в пространстве m, если xn,k=n sin(1/(nk)).
Решение.
Т.к. при x>0 sin x<x, то 0<xn,k<n×1/(nk)£ 1. Поэтому xnÎm. Вычислим пределы координат по первому замечательному пределу:
yk=limn®¥xn,k= limn®¥(1/k × sin(1/(nk))/ (1/(nk)))=1/k.
Т.к. 0<1/k£ 1, то покоординатный предел y={1,1/2,1/3,…}Îm.
В пространстве m
r(xn,y)=supk|xn,k-yk|= supk |n sin(1/(nk)) - 1/k|=
= supkn|sin(1/(nk)) - 1/(nk)|=n supk (1/(nk)-sin(1/(nk))).
Поскольку (x-sin x) /=1-cos x³0, то функция x-sin x монотонно возрастающая. Следовательно,
r(xn,y)=n(1/n-sin(1/n))=1 - n sin(1/n)=1 - (sin(1/n))/(1/n)®0
при n®¥, т.е. xn® y в m.
Проверить сходимость последовательностей xn=xn(t) в функциональных метрических пространствах. В случаях сходимости найти пределы.
Указание 2. Если существует поточечный предел и предел по метрике, то они совпадают.
1.xn(t)=e -nt, 0£ t£ 1, в C[0;1], Cp[0;1], PC[0;1], PCp[0;1] (p³1).
Решение.
Найдём поточечный предел:
при t=0 xn(0)=1, limn®¥xn(0)=1;
при 0<t£ 1 , limn®¥xn(t)= e - ¥ =0.
Итак, поточечно xn(t)®y(t)=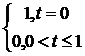
.
Ясно, что yÎPC[0;1], поэтому последовательность xn не является сходящейся в C[0;1] и в Cp[0;1]. В пространстве PC[0;1]
r(xn,y)=sup0£ t£ 1|xn(t)-y(t)|=sup0<t£ 1e -nt=1, limn®¥r(xn,y)=1¹0,
поэтому xn не может сходиться к y в PC[0;1] (нет равномерной сходимости), а тогда, согласно указанию 2, xn вообще не может сходиться в PC[0;1]. В PC[0;1]
r(xn,y)=(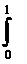
|xn(t)-y(t)|pdt)1/p=(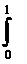e -nptdt)1/p=
=(-1/(np) e -npt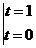
)1/p=(1-e -np)/(np),
limn®¥r(xn,y)=(1-0)/(+¥)=0,
следовательно, xn® y по метрике пространства PCp[0;1].
2.xn(t)=e -nt, 1£ t£ 2, в C[1;2], Cp[1;2], PC[1;2], PCp[1;2] (p³1).
Решение.
Для всякого tÎ[1;2] limn®¥xn(t)= e - ¥ =0, т.е. поточечно
xn(t)®q(t)º0. В пространстве C[1;2]
r(xn,q)=max1£ t£ 2e -nt=e -n, limn®¥r(xn,q)= e - ¥ =0,
поэтому xn®q по метрике C[1;2] (имеет место равномерная сходимость xn к q). Из равномерной сходимости следует сходимость xn®q и по метрике Cp[1;2]. Поскольку C[1;2] и Cp[1;2] являются метрическими подпространствами PC[1;2] и PCp[1;2] соответственно, то и в более широких пространствах PC[1;2] и PCp[1;2] xn®q.
3.xn(t)=te -nt, 0£ t£ 1, в C[0;1], Cp[0;1], C1[0;1], (p³1).
Решение.
При t=0 xn(0)=0, при 0<t£ 1 , limn®¥xn(t)= e - ¥ =0.
Таким образом, поточечно xn(t)®q(t)º0. В равномерной метрике пространства C[0;1] r(xn,q)=max0£ t£ 1xn(t).
Найдём максимум с помощью производной:
xn/(t)=e -nt-nte -nt=(1-nt)/ent, xn/(t)=0 при t=1/n,
при 0£ t<1/n xn/(t)>0, при 1/n<t£1 xn/(t)>0 Þ
Þ max0£ t£ 1xn(t)=xn(1/n)=1/(en).
Тогда limn®¥r(xn,q)=limn®¥(1/(en))=0, и xn®q в C[0;1].
Из равномерной сходимости следует сходимость xn®q в Cp[0;1].
В пространстве C1[0;1]
r(xn,q)=max0£ t£ 1| xn(t)-q(t)|+max0£ t£ 1| xn/(t)-q /(t)|³
³ max0£ t£ 1| xn/(t)|³ | xn/(0)|=1.
Поэтому limn®¥r(xn,q) не может быть равен 0.
Согласно указанию 2, xn не является сходящейся в C1[0;1].
4.xn(t)=åk=0n t k/k! , a£ t£ b, в C[a;b], C1[a;b], C2[a;b].
Решение.
Используя ряд Маклорена et=åk=0¥ t k/k! (-¥<t<+¥), мы получаем поточечный предел: xn(t)®y(t)=et "tÎ[a;b]. Поскольку степенные ряды сходятся равномерно на замкнутых отрезках внутри интервала сходимости, то xn равномерно сходится к y, т.е. xn®y в C[a;b].
Производные xn/(t)=åk=1n t k-1/(k-1)!=åk=0n-1 t k/k!
равномерно сходятся к et=y /(t),
xn//(t)=åk=1n-1 t k-1/(k-1)!=åk=0n-2 t k/k! равномерно сходятся к
et=y //(t), следовательно, xn®y в C1[a;b] и в C2[a;b].
Вообще, xn®y в любом пространстве Cm[a;b] (mÎN).
5.xn(t)=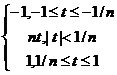
в PC[-1;1], PCp[-1;1] (p³1).
Решение.
Поточечно xn(t)®y(t)=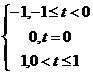 
и yÎPC[-1;1].
В пространстве PC[-1;1]
r(xn,y)=sup-1£ t£ 1|xn(t)-y(t)|=sup0<t<1/n|nt-1|=1,
поэтому сходимость xn к y невозможна, и, согласно указанию 2, xn не является сходящейся в PC[-1;1].
В PCp[-1;1]
r(xn,y)=(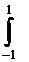
|xn(t)-y(t)|pdt)1/p=(2
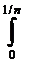|nt-1|pdt)1/p=
=(2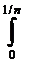(1-nt)pdt)1/p=(-2/n × (1-nt)p+1/(p+1)
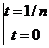)1/p=2/(n(p+1)),
limn®¥r(xn,y)=0,
следовательно, xn®y по метрике PCp[-1;1].
6.xn(t)=1/(1+(nt-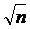
)2) в C[0;1], Cp[0;1].
Решение.
Поточечный предел xn(t)®q(t)º0. В C[0;1]
r(xn,q)=max0£ t£ 1xn(t).
Найдём максимум с помощью производной
xn/(t)= -2n(nt-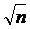)/(1+( nt-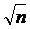)2)=-2n2(t-1/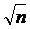)/(1+( nt-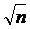)2)2 ,
xn/(t)=0 при t=1/,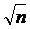
при 0£ t<1/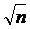 xn/(t)>0, при 1/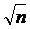<t£ 1 xn/(t)<0,
поэтому max0£ t£ 1xn(t)=xn(1/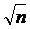)=1/(1+0)=1.
Итак, limn®¥r(xn,q)=1¹0, равномерной сходимости xn к q нет. По указанию 2, xn не является сходящейся в C[0;1].
В Cp[0;1]
r(xn,q)=(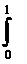|xn(t)-q(t)|pdt)1/p=(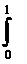(xn(t))pdt)1/p .
Поскольку 0<xn(t)£ 1 и p³1, то (xn(t))p£ xn(t), поэтому
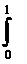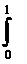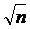r(xn,q)£ ((xn(t))dt)1/p=(1/nd(nt-)/(1+( nt-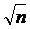)2))1/p=
=(1/n × arctg(nt-)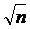
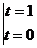)1/p=1/n1/p(arctg(n-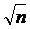)+arctg()).
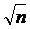Так как величина арктангенс ограниченная, то limn®¥r(xn,q)=0,
и xn®q в метрике Cp[0;1].
7.xn(t)=e t-n в C[0;1], Cm[0;1] (mÎN),Cp[0;1] (p³1).
Решение.
Поточечно xn(t)®q(t)=e - ¥=0. В C[0;1]
r(xn,q)=max0£ t£ 1|xn(t)-q(t)|=max0£ t£ 1(et/en)=e/en,
limn®¥r(xn,q)=0, поэтому xn®q в C[0;1].
Все производные xn/(t)=xn//(t)=…= xn(m)(t)=e t-n
равномерно стремятся к q, поэтому xn®q в Cm[0;1].
Из равномерной сходимости следует и сходимость xn®q по метрике Cp[0;1].
Разные задачи.
1)Доказать, что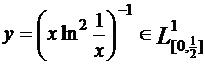 
и не принадлежит 
, 
.
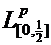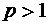2)При каких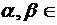 
R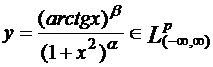 
?
3)Пусть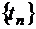 
– числовая последовательность
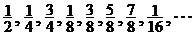
Показать, что последовательность функций
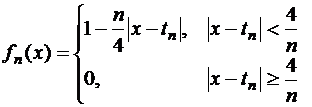
сходится к функции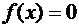 
в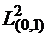 
, но не сходится 
.
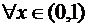4.Найти преобразование Фурье функций
а)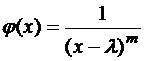 
, 
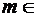N, 
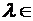С,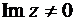 
.
б)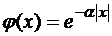 
, (
);
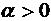в)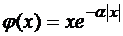 
, () ;
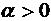г)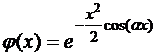 
;
д)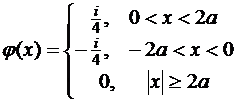 
е)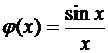 
ж)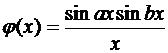 
, (
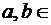R);
з) 
, (
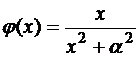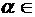R);
5.Найти полную вариацию функции
а)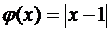 
, 
;
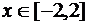б)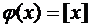 
, 
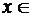[0,5; 3,5];
в)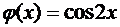 
, ;
6.Вычислить интеграл Стилтьеса
а)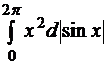 
; б)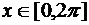 
, 
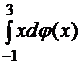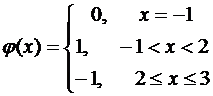
7. Найти норму функционала
а)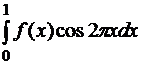 
в пространстве 
.
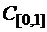б)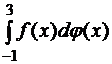 
в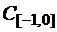 
, функция
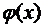та же, что и в примере 6.б.
6. Проверить аксиомы нормированного пространства для пространства матриц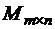 
размера 
:
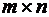а)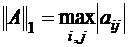 
, б) 
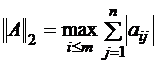, в)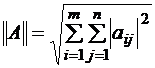 
.
7.Доказать, что пространство 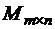банахово в нормах предыдущего примера.
8.Доказать, что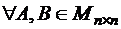 
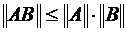(Использовать неравенство Минковского).
9.Доказать, что если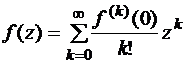 
– целая функция 
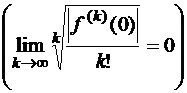, то матричный ряд 
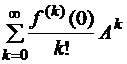сходится абсолютно в банаховом пространстве 
.
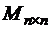10.Вычислить производную Фреше следующих отображений:
а) 
, 
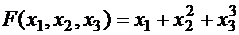в точке 
.
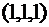б)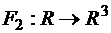 
, 
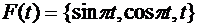в точке 
.
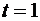в)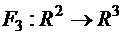 
, 
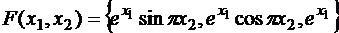в точке 
.
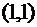г)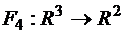 
, 
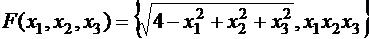в точке
.
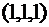11.Вычислить производную Фреше сложного отображения:
а)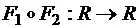 
в точке .
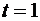б)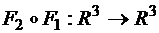 
в точке 
.
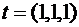в)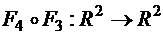 
в точке .
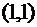г)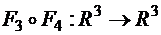 
в точке .
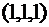12.Найти производную оператора в точке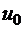 
а)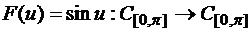 
, 
.
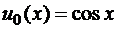б)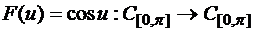 
, 
.
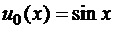в)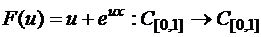 
, 
.
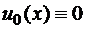г)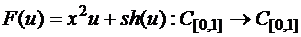 
, .
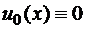д)функционала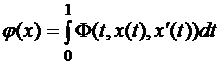 
на пространстве 
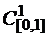непрерывно дифференцируемых на 
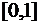, обращающихся в ноль в точках 
, .
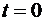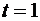13.Вычислить градиент нормы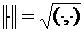 
на элементе 
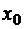в гильбертовом пространстве.
14.Пусть оператор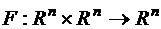 
определяется формулами 
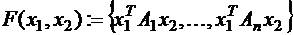, где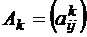 
, размера 
, 
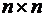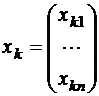. Показать, что он билинейный и ограниченный.
15.Пусть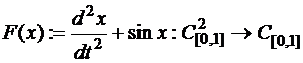 
. Показать, что в точке 
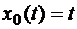первый дифференциал 
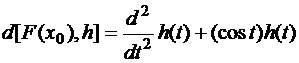, а второй дифференциал 
.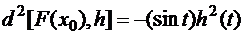