3.2.4. Построение законов управления
План лекции:
1.Две задачи управления.
2.Примеры построения законов управления.
Резюмируя все вышесказанное, можно сформулировать две основные задачи управления:
1. Дать аппроксимацию выходного сигнала к ожидаемому или заданному процессу 
(задача слежения) в каждый момент времени 
.
2. Обеспечить близость выходного сигнала и желаемому постоянному значению 
(задача регулирования).
Тогда естественно ввести в рассмотрение ошибку слежения
(*)
Поставленная задача решена, если 
. Пусть объект управления задан дифференциальным уравнением
,
где 
- управляющее воздействие; 
- возмущенная.
С учетом (*) уравнение принимает вид:
.
Управляющее воздействие является решением уравнения.
,
а ошибка управления совпадает с решением однородного уравнения 
при нулевых начальных условиях. Но тогда, очевидно 
.
Рассмотрим пример построения законов уравнения.
ПРИМЕР 1. Объект представляет из себя апериодическое звено 
, 
и требуется осуществить слежение на процессом 
.
Тогда 
, где 
, и, следовательно
, 
- управляющее воздействие пропорционально единичному ……….. и учитывает постоянную времени звена 
.
ПРИМЕР 2. Требуется сохранить устойчивость для объекта, описывающего колебательное звено
при начальных условиях 
, 
при наличии возмущения 
. Так как в силу начальных условий 
, то
,
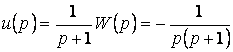общая оригинале 
дает вид управляющего воздействия.
Вот пример построения управления с помощью обратной связи.
ПРИМЕР 3. Пусть теперь в рассмотренном выше уравнении объекта управления управляющее воздействие имеет вид:
.
Здесь 
- есть сигнал обратной связи, вырабатываемый на основе полученных измерений выхода, а второе слагаемое не зависит от 
.
Пусть обратная связь линейна 
, где 
.
Подставляет это в уравнение объекта, получим
.
И, таким образом
Введение обратной связи по выходу и его ………… позволяется изменять характеристический многочлен системы: вместо исходного 
получаем
.
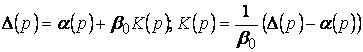Пусть 
- произвольный устойчивый многочлен. Тогда при выборе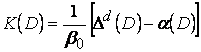 
система с обратной связью окажется устойчивой.
Пусть объект описан уравнением
, 
.
Исходный объект не является устойчивым, так как его характеристический многочлен 
имеет корни 
, 
.
Введем обратно связь 
.
Тогда выход будет изменяться согласно уравнению 
, а характеристическое уравнение системы с обратной связью имеет вид 
.
Выберем коэффициент усиления 
, 
, 
так, чтобы все корни многочлена были одинаковы: 
, 
,
т.е.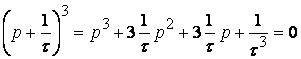 
.
Уравнением у многочленов коэффициента при одинаковых степенях, предварительно умножив обе части полученных уравнений на , будем иметь:
; 
; 
.
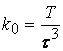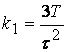Варьируя величину параметра 
, можно добиться различных способов сглаживания выхода в зависимости от ненулевых начальных условий.
Контрольные вопросы:
1.В чём состоит задача сложения?
2.В чём состоит задача регулирования?
3.Уравнения для управляющего воздействия и ошибки управления.