1.2.1. Алгебраические критерии устойчивости по начальным условиям
План лекции.
1. Установившаяся реакция и частотная характеристика.
2. Соединение с обратной связью и проблема устойчивости.
Рассмотренный выше случай, когда все нули многочлена имеют отрицательную вещественную часть, доставляет нам случай установочного многочлена, или многочлена Гурвица. Существуют различные критерии устойчивости многочлена, наиболее простым из которых является критерий Стодоян. Если многочлен 
устойчив, то все его коэффициенты положительны. Доказательство очевидным образом следует из разложения многочлена на множители.
ПРИМЕР. Многочлен 
неустойчив, так как 
.
Звено называется устойчивым по начальным условиям, если вызываемый ими эффект 
исчезает при 
. Преобразование Лапласа ранее применялось нами при нулевых начальных условиях. При произвольных начальных условиях вид решения изменяется.
Из теории дифференциальных уравнений известно, что общее решение может быть записано как сумма решений однородного уравнения 
и любой части решения неоднородного уравнения 
.
Тогда (**)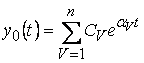 
, где 
- корни характеристического многочлена , а 
- либо ………., либо многочлен от 
. С учетом этого общее решение приобретает вид
.
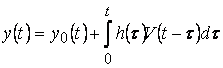Из формулы (**) сразу вытекает следующий результат.
Критерий устойчивости по начальным условиям. Неустойчивость по начальным условиям имеет место, если характеристический многочлен не имеет других корней, кроме корней с отрицательной вещественной часть, т.е. 
является устойчивым. Очевидно, что приведенный критерий устойчивости по начальным условиям совпадает с условием устойчивости по входу, так что при выполнении обоих условий употребляется термин «устойчивое звено».
3.2.3. Устойчивая реакция и частотная характеристика
Устойчивой реакцией на заданное воздействие 
, 
такую функцию 
, что
,
где 
- решение, найденное при нулевых начальных условиях.
Пусть входное воздействие является гармоническим, т.е.
, 
,
где 
- амплитуда; 
- частота воздействия.
ТЕОРЕМА 1. Если звено является устойчивым, то установившаяся реакция на гармоническое воздействие является гармонической функцией той же частоты с амплитудой 
и относительным сдвигом фазы 
.
Рассмотрим реакцию на комплексную гармонику 
, . Тогда, очевидно,
.
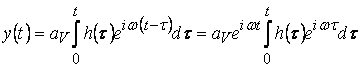Если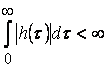 
, то существует предел 
.
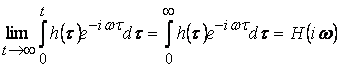Тогда функция 
является установившейся реакцией на комплексную гармонику. Тогда, отделим вещественную и мнимую части, и уровни соответствующие оценки, получим утверждение ………
ПРИМЕР.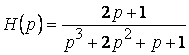 
, 
.
Многочлен в знаменателе устойчив, 
, 
, поэтому
,
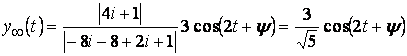где 
.
Рассмотрим теперь установившуюся реакцию на номинальное воздействие вида
, .
Справедлива.
ТЕОРЕМА 2. Установившаяся реакция устойчивого звена на полиномиальное воздействие также является полиномом и допускает представление!
, где 
, 
.
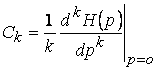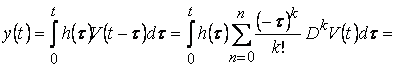
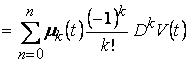, где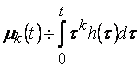 
, где тейлоровское разложение функции имеет конечное число слагаемых.
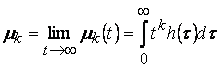называют моментальной высотой функции.
Но тогда установившаяся реакция будет иметь вид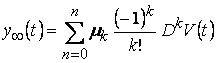 
, что и доказывает теорему, поскольку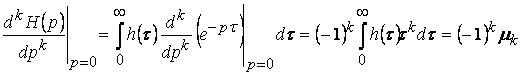 
В частности, если входное воздействие постоянно, т.е. 
, , то установившаяся реакция устойчивого звена также постоянна и равна 
. Воздействие остается неизменным, если 
.
Если же входное воздействие линейно, т.е. 
, , то установившаяся реакция устойчивого звена также меняется с постоянной скоростью
.
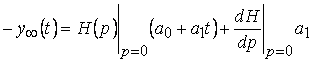Если, кроме того, выполнено условие , то 
.
Если в рассмотренном выше примере передаточная функция не изменяется, а на вход подается сигнал 
. Поскольку , 
, 
.
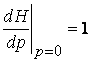3.2.3. Соединения с обратной связью и проблема устойчивости
Структурная схема соединения с обратной связью имеет вид:
Звено 1 именуется стоящее в простой цепи, звено 2 – стоящее в обратной связи. Тогда, как известно ( ), передаточная функция соединения имеет вид
.
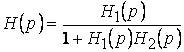Если в случае коррекции динамических исследований операторное уравнение звена имело вид 
, то в звене с отрицательной обратной связью вычитается некоторая функция 
! Пропорциональная входному воздействию: 
, 
.
Здесь 
- ограниченный линейный оператор, а 
- ……… числовой параметр. Соответствующее однофазное уравнение 
всегда имеет тривиальное решение уравнения могут быть переписаны в виде
и 
.
Тогда если 
: оператор 
обратим, то соответствующий обратит оператор 
называется резольвент; тогда для каждого такого значения уравнение звена с обратной связью имеет решение 
. В этом случае однородное уравнение имеет только тривиальное решение.
Такие значения называют регулярными.
!Множество всех значений , при которых оператор необратим, называется спектром оператора . Особый интерес представляет значение , доставляющее нетривиальное решение однородному уравнению. Такие называют собственными значениями оператора , а соответствующее решение – собственной функцией оператора . Очевидно, что все собственное значение принадлежит спектру. Однако структура его может быть и совершенно нет.
Рассмотрим в качестве примера оператор 
в пространстве 
.
, поэтому ……. Этого оператора имеет вид 
, очевидно, что уже влево 
оператор ……….., поэтому его спектр заполняет отрезок 
. Однако собственных значений у этого оператора нет, так как уравнение 
имеет только тривиальное решение 
.
Рассмотрим типичное соединение с обратной связью на рис. ( )
Задачей этой системы является воспроизведение выходным сигналом 
любых измерений сигнала 
. С этой целью в устройстве формируется сигнал ошибки 
, который затем подвергается усилению и подается на вход регулируемого объекта . Выходной сигнал 
снова подается на вход по цепи обратной связи. Тогда уравнение рассматриваемой системы принимает вид:
,
или, если переобозначить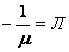 
, 
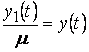, получим рассмотренное выше уравнение 
.
Если существует резольвента этого уравнения 
, можно определить сигнал ошибки 
. Его оценка по норме имеет вид:
.
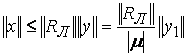Выходной сигнал, очевидно, будет с большой точностью воспроизводить любое измерение входного сигнала , если 
будет сколь угодно малым, а это и означает, что система с обратной связью должна быть устойчивой. Это как мы видим выше, сводится к ограниченности по модулю передаточной функции 
, т.е.
.
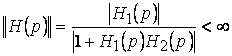Контрольные вопросы:
1.Какой многочлен называется многочленом Гурвица?
2.Определение устойчивости по начальным условиям.
3.Критерий устойчивости по начальным условиям.
4.Установившиеся реакции на гармонические воздействия.
5.Установившиеся реакции на полиномиальные воздействия
6.Что такое спектр оператора?
7.Резольвента соединения с обратной связью.