3.2. Спектральные свойства операторов и систем с обратной связью
1.2.1. Устойчивость звена по входу
1.2.2. Алгебраические критерии устойчивости по начальным условиям.
Звено называется устойчивым по входу, если при любом ограниченном входном воздействии 
и нулевых начальных условиях выходная реакция 
является ограничением 
и называется неустойчивым в противном случае.
Критерий устойчивости по входу дает интерес от весовой функции. Справедлива следующая теорема.
ТЕОРЕМА 1. Для того чтобы звено, описываемое уравнением 
было устойчивым входу, необходимо и достаточно, чтобы выполнялось условие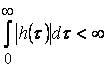 
(*).
Необходимость.
От противного, предположим, что условие (*) нарушено, т.е. несобственный интерес расходится. Пусть на вход подается входное воздействие
где 
достаточно большое положительное число, а 
- неполная константа. Тогда
.
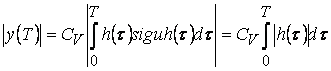Если интервал неограничен, то и функция 
неограничена, что противоречит предположению.
Достаточность.
Пусть произвольная ограниченная функция, т.е. такая, что 
, 
, 
.
Тогда
.
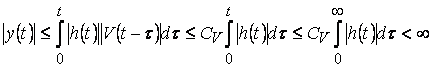Используя полученную оценку, нетрудно выработать критерий устойчивости по передаточной функции.
ТЕОРЕМА 2. Для выполнения условия (*) необходимо и достаточно, чтобы передаточная функция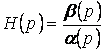 
была ограничена по модулю для 
.
Необходимость.
Поскольку весовая функция есть оригинал для 
, т.е.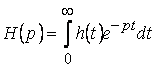 
, справедлива следующая оценка:
,
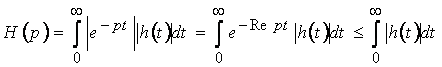так как 
, 
, .
Достаточность.
Пусть 
, 
- корни многочлена 
. Рассмотрим случай различных корней. Тогда справедливо алгебраическое представление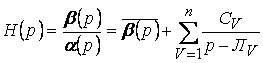 
, 
.
Ограниченность означает, что:
1) 
, т.е. степень многочлена 
не выше степени ;
2) 
.
Тогда оригинал от передаточной функции, т.е. весовая функция звена, имеет вид:
.
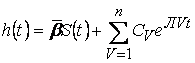Проверим критерий устойчивости по входу:
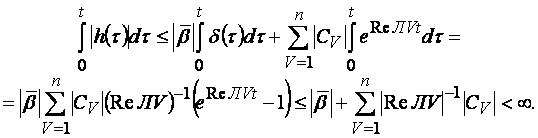
В случае кратких полюсов выкладки более громоздки.
Резюмируя все вышесказанное, можно сформулировать
Критерий устойчивости по входу. Устойчивость по входу имеет место, если выполнено два условия:
а) степень многочлена в знаменателе не меньше степени многочлена в числителе;
б) многочлен , т.е. характеристический многочлен звена не имеет других корней, кроме корней с отрицательными вещественными частями.
Рассмотрим критерии устойчивости на примере простейших типовых звеньев ( ).
1. Идеальный усилитель 
, 
, корней нет.
2. Интегратор 
, 
, 
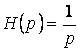, один вещественный корень 
.
3. Апериодическое звено: 
, 
, 
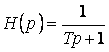, один вещественный корень 
, при 
.
4. Колебательное звено 
, 
имеет два комплекско-сопряженных корня 
, причем 
.
Таким образом, все эти звенья устойчивы по входу за исключением интегратора. Это очевидно и из поведения его переходной функции, которая, являясь реагирует на ограниченное воздействие, неограниченно растет.
Контрольные вопросы:
1. Какое звено называется устойчивым по входу?
2. Каково условие устойчивости по входу?
3. Критерии устойчивости по передаточной функции.
4. Устойчивость простейших типовых звеньев: идеальный усилитель, интегратор, апериодическое звено, колебательное звено.