Глава 3. ОПЕРАТОРЫ И ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ.

ПОСТРОЕНИЕ ЗАКОНОВ УПРАВЛЕНИЯ

 

Лекция №6.

3.1. Обратные ожидания и сглаживание динамических искажений

План лекции:

1.Обратные операторы и сглаживание динамических искажений.

2.Задачи, сводящиеся к операторным уравнениям и их разрешимость.

3. словия ограниченности обратного оператора в динамических системах с дробно-рациональной передаточной функцией.

Пусть  - функциональное пространство, и - множество всех линейных агрегатов над . В этом множестве определена операция  умножения , обладающая свойством ассоциативности и дистрибутивности:

,  ,  ,

так что для вашего отрезка  существует единичный отрезок .

Если - скаляр, то ; ; .

Множество операторов над функциональным пространством образует кольцо с единицей. Это кольцо может быть и нормированным, причем .

Целый ряд задач управления сводится к решению операторных уравнений типа , где , а также проблема однозначных таких решений. С этой целью в рассмотрение вводится обратный оператор , т.е. такой, что , где  - тождественный оператор. В самом общем случае это означает, что если отображение  биситивно, то существует линейный и ограниченный обратный оператор . Нарушение в дальнейшем однозначно лежит правда и неограниченном обратно оператора.

Во многих технических задачах, связанных с трансформацией сигнала через систему, возникают задачи определения обратно оператора.

Если нужно восстановить первоначальную форму сигнала , называемую на вход система, то это может быть достигнуто с помощью корригирующей системы с оператором , как показано на рис.1.

                                   

Рис.1.

Примером реализации подобных случаев может быть динамическая система, описываемая дробно-рациональной передаточной функцией. В зависимости от того, является эта рациональная дробь правильной или неправильной, обратный оператор может быть неограничен или органичен.

Пусть непередаточная функция – неправильная дробь:

,

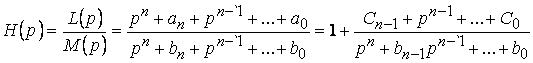где многочлены  и  имеют нули в левой полуплоскости, т.е. если , то функции  и  аналитические и ограниченные. Тогда оператор, дающий преобразование «вход-выход» имеет вид:

,

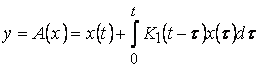где  есть обратное преобразование Лапласа функции .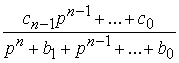

Этот оператор имеет непрерывное ядро и действует в пространстве непрерывных функций, являясь при этом ограниченным оператором.

Обратный оператор 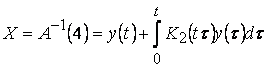. Ядро этого оператора

является обратным преобразованием Лапласа правильной части рациональной дроби

.

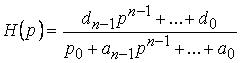Если передаточная функция изначально является правильной рациональной дробью, а ее числитель имеет нули, расположенные в правой полуплоскости, обратный оператор такой системы становится неограниченным. Поскольку неограничение оператора практически трудно реализуется, для корреляции динамических искажений используют добавление звена с обратной связью.

 

Контрольные вопросы:

1.Как определена операция умножения в функциональном пространстве линейных операторов?

2.Каковы условия ограниченности обратного оператора для системы с передаточной функцией в виде рациональной дроби?

3.Как корректировать динамические искажения с целью восстановления первоначального сигнала.