Линейные преобразования случайного процесса
Случайный процесс есть
семейство величин, зависящих от времени как от параметра. Если зафиксировать
одно из возможных значений из случайных величин, то получим некоторую
неслучайную, детерминированную функцию времени, реализацию случайного процесса.
Таким образом, ![]() можно
рассматривать как совокупность реализаций, для которой определены общие вероятностные
характеристики. Постоянными из них являются математическое ожидание
можно
рассматривать как совокупность реализаций, для которой определены общие вероятностные
характеристики. Постоянными из них являются математическое ожидание ![]() , дисперсия
, дисперсия ![]() и корреляционная
функция
и корреляционная
функция ![]() . Если
для случайного процесса
. Если
для случайного процесса ![]() заданы только его математическое ожидание
и корреляционная функция, то говорят, что он описан в системе корреляционной теории:
заданы только его математическое ожидание
и корреляционная функция, то говорят, что он описан в системе корреляционной теории:
![]() ;
;
![]() .
.
Если ![]() ,
, ![]() , то процесс называется стационарным в
широком смысле. Для стационарного процесса
, то процесс называется стационарным в
широком смысле. Для стационарного процесса ![]() .
.
Если 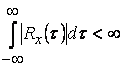 , то существует преобразование
Фурке корреляционной функции
, то существует преобразование
Фурке корреляционной функции
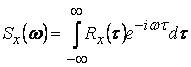 .
.
Функция ![]() называется специальной
плотностью процесса
называется специальной
плотностью процесса ![]() .
Корреляционная же функция может быть найдена как обратное преобразование Фурке:
.
Корреляционная же функция может быть найдена как обратное преобразование Фурке:
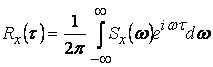 .
.
В случае стационарного случайного процесса
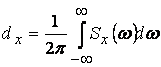 .
.
Если входное воздействие ![]() является случайным, то
линейным сигналом
является случайным, то
линейным сигналом
![]() , где
, где ![]() ,
, ![]() - детерминированный функции, также являются
случайным процессом. Тогда его характеристика:
- детерминированный функции, также являются
случайным процессом. Тогда его характеристика:
![]() ;
;
![]() .
.
Пусть теперь случайный процесс записан в виде интегрального преобразования, как было рассмотрено выше:
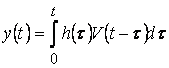 .
.
Если входное воздействие стационарно, то
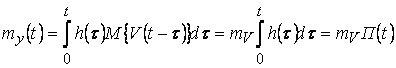 .
.
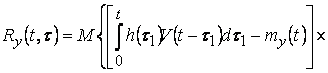
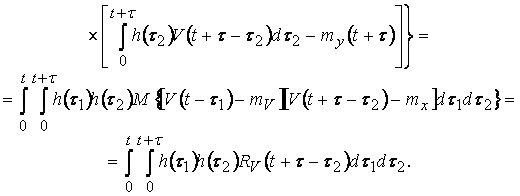
Итак, если линейное звено
характеризуется своей весовой функцией, то по заданному входному воздействию и
корреляционной функции входа можно описать случайный процесс в сигнале
корреляционных теорий. Значительный интерес представляет также случайная
теорема. Пусть ![]() стационарный
случайный процесс и
стационарный
случайный процесс и 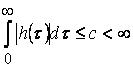 .
Тогда
.
Тогда 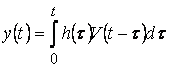 имеет
корреляционную функцию устанавливается реакции
имеет
корреляционную функцию устанавливается реакции ![]() и спектральную плотность выходного сигнала
и спектральную плотность выходного сигнала
![]() ,
,
где ![]() - спектральная плотность
- спектральная плотность ![]() , а
, а ![]() - частотная характеристика
преобразования
- частотная характеристика
преобразования
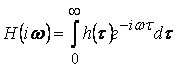 .
.
Так как ![]() ,
, ![]() , можно убедиться, что
, можно убедиться, что ![]() ограничена при
ограничена при ![]() , откуда следует
существование процесса
, откуда следует
существование процесса ![]() , причем
, причем
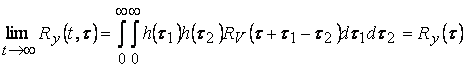 .
.
Спектральная плотность выходного сигнала при этом
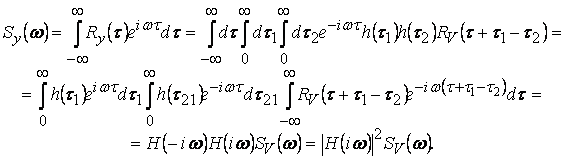
Запишем также, дисперсия выходного сигнала
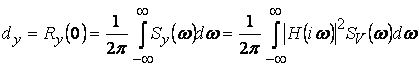 .
.
Легко видеть, что управляя случайным сигналом для получения заданных характеристик можно изменить характеристики входного сигнала (дисперсию, матожидание, корреляционную функцию) или передаточную функцию звена, т.е. его дифференциальное уравнение.
Выше уже отмечалось, что
сигналы, поступающие на вход линейный системами, можно считать элементами
гильбертовых пространств с нормой ![]() .
.
Выясним, каким образом
специальная плотность связана со спектрами отдельных реализаций стохастического
процесса. Введем в рассмотрение функцию ![]() -реализации …………. Процесса
продолжительности
-реализации …………. Процесса
продолжительности ![]() :
:
![]()
Амплитудно-частотная характеристики этой функции
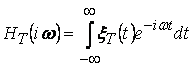 .
.
Рассмотрим функцию 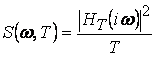 - специальное
распределение мощности сигнала
- специальное
распределение мощности сигнала ![]() и вычислим ее математическое ожидание.
и вычислим ее математическое ожидание.
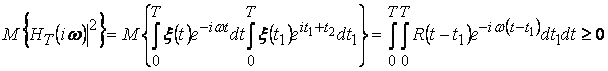 . Пусть
. Пусть ![]() , тогда интеграл равен сумме двух
интегралов
, тогда интеграл равен сумме двух
интегралов
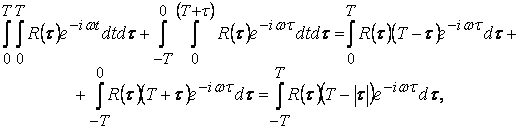
откуда будем иметь асимметрически!
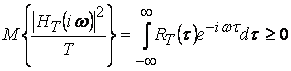 ,
,
где
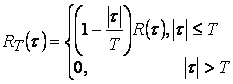
В пределе, очевидно ![]() и, следовательно:
и, следовательно:
![]() .
.
С учетом соотношения 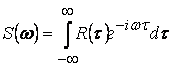 легко найти специальную
плотность процесса с известной корреляционной функцией. Например, для стационарного
случая процесса с корреляционной функцией
легко найти специальную
плотность процесса с известной корреляционной функцией. Например, для стационарного
случая процесса с корреляционной функцией
![]()
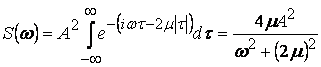 .
.
Если в частности, отношение ![]() уже
уже ![]() имеет предел, то функция
имеет предел, то функция ![]() выражается в
выражается в ![]() - функция Дирахка, а
- функция Дирахка, а ![]() . Процесс с постоянным
энергетическим спектром и нескорреляционными оценками называют б….. шумом.
. Процесс с постоянным
энергетическим спектром и нескорреляционными оценками называют б….. шумом.
В том случае, если стационарный случайный сигнал
является дискретным, его тоже можно рассматривать как элемент гильбертова
пространства ![]() с
нормой
с
нормой
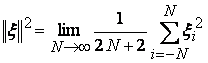 , где
, где ![]() ,
, ![]()
Скалярное уравнение
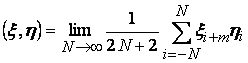
определяет взаимную корреляционную функцию ![]() дискретных случайных
сигналов составляющими
дискретных случайных
сигналов составляющими ![]() ,
, ![]() .
.
Контрольные вопросы:
1.Какие характеристики описывают случайный процесс в смысле корреляционной теории?
2.Что такое спектральная плотность случайного процесса?
3.Каковы входные характеристики линейного случайного сигнала?
4.Запишите частотную характеристику в виде интегрального преобразования.