Глава 2. ПРЕОБРАЗОВАНИЕ СИГНАЛОВ ЛИНЕЙНОЙ СИС0-ТЕМОЙ
План лекции:
1.Преобразование сигналов линейной системы «вход-выход»
2.Операционный метод анализа линейных систем.
2.1. Соотношение «вход-вывод»
Системный подход, широко используется для описания процессов, происходящих в технических устройствах (и не только в технических), является наиболее общим методом построения математических моделей с возможностью предсказания результата на заданное воздействие. Технологический процесс может состоять из ряда этапов, или звеньев, описываемых тем или иным дифференциальным уравнением (системой дифференциальных уравнений». Если дифференциальное уравнение линейное, то и система называется линейной. Система, не являющаяся линейной, может быть в ряде случаев ……неорудована ( ). Звено системы осуществляет преобразованное одного процесса, называемого входным воздействием, в другой, называемый выходным реакцией или преобразователем «вход-вывод». Взаимодействия между звеньями определяет уже структуру системы.
2.2. Операционный метод анализа линейных систем
Пусть для описания линейных систем может быть построено линейное дифференциальное уравнение
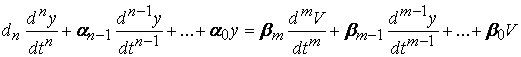 . (2.2)
. (2.2)
Вводя в рассмотрение оператор дифференцирования ![]() , запишем уравнение (2.1) в операторной форме
, запишем уравнение (2.1) в операторной форме
![]() , (2.3)
, (2.3)
где ![]() ;
;
![]() .
.
Тогда 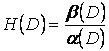 называется операторной передаточной функцией или оператором звена ( ).
называется операторной передаточной функцией или оператором звена ( ).
Известно, что оператор Лапласа 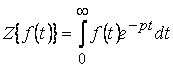 при нулевых начальных условиях
при нулевых начальных условиях ![]() , обладаем ………..
, обладаем ……….. ![]() .
.
Подействуем оператором Лапласа на обе части уравнения (2.3): ![]() , где
, где ![]() ,
, ![]() , откуда легко видеть, что комплексное передаточная функция звена находится как отношение
, откуда легко видеть, что комплексное передаточная функция звена находится как отношение ![]() -образов входа и выхода при нулевых начальных условиях.
-образов входа и выхода при нулевых начальных условиях.
![]() .
.
Она может быть получена из операторий заменой оператора дифференцирования на комплексную переменную ![]() .
.
Таким образом, передаточная функция
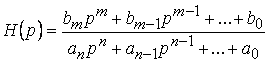
является рациональной дробью с действительными коэффициентами ![]() ,
, ![]() . Эта функция аналитическая и ограниченном в правой полуплоскости, а ее полюсы расположены в левой полуплоскости или на нижней оси. Передаточная функция зависит от комплексной частоты
. Эта функция аналитическая и ограниченном в правой полуплоскости, а ее полюсы расположены в левой полуплоскости или на нижней оси. Передаточная функция зависит от комплексной частоты ![]() ; в частности, если
; в частности, если ![]() ,
, ![]()
![]() , где
, где ![]() называют амплитудной характеристикой, а
называют амплитудной характеристикой, а ![]() - фазовой характеристикой. Функция
- фазовой характеристикой. Функция ![]() характеризует уменьшение амплитуды синусоидального сигнала с частотой
характеризует уменьшение амплитуды синусоидального сигнала с частотой ![]() при прохождении его через систему, а
при прохождении его через систему, а ![]() описывает соответствующее смещение фазы того сигнала.
описывает соответствующее смещение фазы того сигнала.
Функцию ![]() называют амплитудно-частотной характеристикой звена.
называют амплитудно-частотной характеристикой звена.
Если ![]() - финишная передаточной функции
- финишная передаточной функции ![]() , то
, то 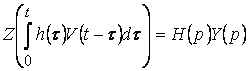 , где
, где ![]() ,
, ![]() , откуда
, откуда 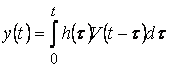 , что дает явное выражение для преобразования вход-вывод через весовую функцию звена
, что дает явное выражение для преобразования вход-вывод через весовую функцию звена ![]() , с помощью которой взвешиваются значения входной переменной в целом в момент
, с помощью которой взвешиваются значения входной переменной в целом в момент ![]() для того, чтобы суммируясь, сформировать значение выхода в текущий момент
для того, чтобы суммируясь, сформировать значение выхода в текущий момент ![]() .
.
С помощью этого соотношения легко рассчитать реакцию на любое входное воздействие.
Особый интерес представляет случай, когда это входное воздействие имеет вид функции Хевисайда, т.е. един…. Слайд:
![]() .
.
Реакцию звена на такое воздействие называют со переходной функцией 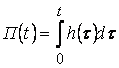 , а ее изображение, очевидно,
, а ее изображение, очевидно, 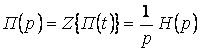 .
.
Уместно отметить, что в случае тождественного пре….дования ![]() справедливо соотношение
справедливо соотношение
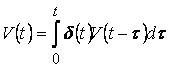 ,
,
так что ![]() - функция есть весовая функции тождественно преобразования.
- функция есть весовая функции тождественно преобразования.
Итак, любая из функций ![]() ,
, ![]() ,
, ![]() полностью характеризует функционирование звена как преобразование вход-выход при нулевых начальных условиях.
полностью характеризует функционирование звена как преобразование вход-выход при нулевых начальных условиях.
Контрольные вопросы:
1.Определить передаточную функцию звена.
2.Что называется весовой функцией звена?
3.Запишите преобразования «вход-выход» в виде свёртки весовой функции и входного воздействия.
4.Что представляет собой реакция звена на единичный скачок?