План лекции:
1.Гильбертово пространство.
2.Случайные сигналы как элементы гильбертова пространства.
1.3. Гильбертово пространство
Если в 
-мерном вектором пространстве 
ввести скалярное произведение, оно превращается в евклидово 
. Если аналогично выделить класс линейных пространств с элементами произвольной природы, в которых определенным образом задано скалярное перемножение, то такие пространства называют Гильбертовыми. Пространству Гильберта соответствует следующая система аксиом:
1.
-линейное пространство произвольной природы.
2.
соответствует вещественное или комплексное число 
, называемое Скалярным произведением, удовлетворяющее следующим условиям:
а) 
;
б) 
;
в) 
;
г) 
. Число 
называют нормой элемента 
.
3. Пространства полное, т.е. каждая функциональная последовательность имеет в нем предел.
Из рассмотренных выше пространств состояний наиболее простым примером гильбертова пространства является 
, где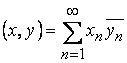 
, причем для любого элемента 
ряд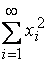 
сходится.
Метрина определяется формулой
.
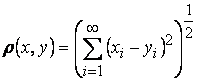Известно, что пространство 
полно 
, откуда и следует гильбертовость.
Пространство или 
является дискретной моделью пространства состояний беско…….. мерной системы. Пространство 
является удобной моделью системы с непрерывными состояниями. - гильбертово пространство, если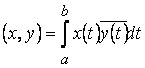 
. Свойства а)-г) легко усматриваются из свойств интеграла Лебега. Можно показать, что пространство 
полно для .
Метрина может быть введена формулой:
.
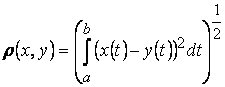1.4. Случайные сигналы как элементы гильбертовых пространств
Входные сигналы, преобразующие современными техническими системами, крану редко носят детерминированный характер. Случайный сигнал может быть определен как измеримое преобразование пространства элементарных событий в ось вещественных чисел. Тогда под распределением вероятностей случайного сигнала 
будем понимать следующую функцию:
W. Это означает, что для каждого измеримого множества 
определена вероятность того, что случайная функция принимает значения, принадлежащие этому множеству. Далее легко определяется функция распределения (1) : 
, математическое ожидание (1) 
по вероятностной мере, или, что то же,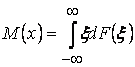 
.
Таким образом, определено измеримое преобразование 
пространства элементарных событий 
в функциональное пространство 
. При каждом фиксированном 
получаем функцию 
, называемую реализующей случайного процесса. Поскольку случайные процессы протекают во времени, 
, то мат.ожидание принимает вид:
.
Этот интеграл, зависит от времени, называется интегралом Бохнера.
Интеграл Бохнера существует, если пространство содержит счетное всюду плотное подмножество, а суммарная площадь, ограниченная амплитудами 
, конечна:
,
где - норма (амплитуда) случайного сигнала в пространства .
Наблюдение за случайными процессами, принимающими в одних и тех же условиях, приводят к известной идеализирующие этих процессов, предполагающей «однородность» этих процессов времени. Такие процессы принять называть стационарными. Для стационарных случается функции все одномерные функции распределения не зависят от времени, а двумерное могут зависеть только от разности 
, т.е. 
.
Корреляционная теория стационарных случайных процессов опирается на вычисление двух основных характеристик математического ожидания 
и корреляционной функции 
. Такая идеализация не может полностью описать все свойства процесса, но значительно упрощает описание случайных процессов с гауссовыми распределениями, наиболее распространенных на практике. Структура корреляционной функции позволяет дать ей следующее толкование. Сигналы 
можно считать элементами гильбертова пространства с нормой 
, т.е. дисперсией случайного сигнала. Корреляционная функция является в этом случае скалярным произведением и 
=
, т.е. 
.
Контрольные вопросы:
1.Система аксиом в пространстве Гильберта.
2.Интеграл Бохнера как измеримое преобразование.
3.Как определяется норма и скалярное произведение в гильбертовом пространстве случайных сигналов.