План лекции:
1.Мера и измеримость. Пространство функций, интегрируемых в смысле Лебега.
2.Системы множеств. Кольца и алгебры множеств.
3.Мера на кольцах.
4.Измеримые функции.
5.Интегралы Лебега.
1.2. Мера и измеримость.
Пространства функций интегрирующих в ……. Лебега
Известно, что основой языка современной математики является теория множеств. Георг Кантр впервые ввел в математику понятие эквивалентных множеств как получающихся одно из другого в результате биактивного отражения. Это послужило основой для определения мощности множества. С позиций конторовской теории гипотеза и контрпрямоугольного треугольника содержат одинаковое число точек, т.е. эквиваленты. Однако есть нечто, что отнимает гипотезу к ……… - это длина, т.е. мера.
Для точного определения меры и измеримости нам понадобится вспомогательные определения.
Системой множеств называется всякое множество, элементы которого сами представляют собой какие-либо множества.
Система множеств ![]() называется концом, если она удовлетворяет следующим условиям:
называется концом, если она удовлетворяет следующим условиям:
1) ![]() Æ
Æ
2) если ![]() ,
, ![]()
![]() ,
, ![]() .
.
Отсюда следует, в частности, что:
1. ![]() ,
,
2. Æ![]() , так как
, так как ![]() Æ.
Æ.
Множество I называется единицей системы множеств ![]() , если:
, если:
1) ![]()
2) из того, что ![]()
Комуо множеств с единицей называется алгеброй множеств.
Таким образом, каждое комуо содержит пустое множество, а также сумму и произведение любого конечного числа своих элементов.
Комуо множеств называют ![]() -коумом, если вместе со счетной последовательностью
-коумом, если вместе со счетной последовательностью ![]() оно содержит счетную сумму
оно содержит счетную сумму 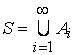 .
.
Поскольку интуитивно ясно, что понятие меры обобщаем понятие длины, площади и объема, целесообразно определить меру на элементарных множествах.
Множество ![]() {
{![]() , где
, где ![]() } назовем элементарным прямоугольником в
} назовем элементарным прямоугольником в ![]() . Естественно считать, что мера
. Естественно считать, что мера 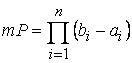 .
.
Справедливо следующее утверждение. Множество ![]() , представляющее собой совокупность множеств в
, представляющее собой совокупность множеств в ![]() , представленных в виде конечного объединения ………….. прямоугольников
, представленных в виде конечного объединения ………….. прямоугольников ![]() - кольцо:
- кольцо: 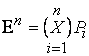 . Назовем его элементарным множеством.
. Назовем его элементарным множеством.
Ясно, что при ![]() элементарный прямоугольник превращается в отрезок, мера его – длина; при
элементарный прямоугольник превращается в отрезок, мера его – длина; при ![]() элементарный прямоугольник – плоский прямоугольник, его мера – площадь; при
элементарный прямоугольник – плоский прямоугольник, его мера – площадь; при ![]() элементарный прямоугольник - параллелепипед, его мера – объем.
элементарный прямоугольник - параллелепипед, его мера – объем.
Мерой элементарного множества ![]() будет называть
будет называть
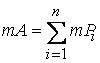 .
.
Идеологически очевидно понятие меры распространяется на любые множества и берется по всевозможным исчерпыванием множества конечными или счетными системами прямоугольников.
Итак, мерой ![]() называют…………… среднеедином определении на кольце множеств
называют…………… среднеедином определении на кольце множеств ![]() , для которого выполнение условия:
, для которого выполнение условия:
1. ![]() , если
, если ![]()
2. ![]() Æ
Æ
3.если ![]() - система множеств:
- система множеств: 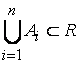 , то
, то 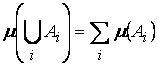 (В частности, система
(В частности, система ![]() может быть и счетной, и тогда мера определяется на
может быть и счетной, и тогда мера определяется на ![]() -кольце. Свойство
-кольце. Свойство  носит название счетной аддитивности меры).
носит название счетной аддитивности меры).
В частности, множества континуальной природы, очевидно приемлемы, а счетные множества имеют меру нуль. Каждое счетное множество является множеством ……… категории и множеством нуль.
Будем говорить, что некоторое условие выполняется почти всюду, если оно справедливо всюду, за исключением множества меры нуль.
Из определения меры следуют следующие свойства меры:
1. Если ![]() , причем
, причем ![]() , то
, то ![]()
2. Если ![]() , то
, то ![]() .
.
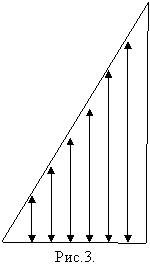
Сигналы, поступившие на вход динамических систем, носят часто ступенчатый характер, или моделируются, как мы видим, счетными последовательностями, поэтому возникает необходимость в более общем понятии интеграла от измерений функции, чем интеграл Римана.
Функцию ![]() называем измерением, если
называем измерением, если ![]()
![]()
![]() измеримое множество
измеримое множество ![]()
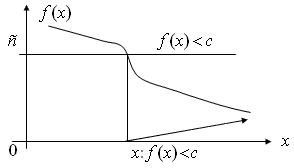
Рис.4
Из определения измеримости легко ус………..ваются следующие свойства:
1) непрерывная функция измерима;
2) композиция непрерывной и измеряет функции измерима;
3) измеримость – инертное свойство, т.е. функция ![]() - измерима;
- измерима;
4) произведение и частное измеримых функций измеримо.
Пусть ![]() измерима на отрезке
измерима на отрезке ![]() со значениями в
со значениями в ![]() , так что
, так что ![]()
Пусть ![]() .
.
Назовем интегральной суммой 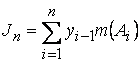 - приведенная мера множества
- приведенная мера множества ![]() на напряженное число
на напряженное число ![]() из соответствующих отрезков.
из соответствующих отрезков.
Интегралом Лебега функции ![]() на отрезке
на отрезке ![]() называется точная верхняя грань суммы
называется точная верхняя грань суммы ![]() :
:
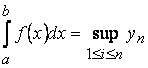 .
.
Нижние интегральные сумму существуют, так как в силу измеримости функции выражение ![]() имеет ……………..
имеет ……………..
Из очевидной оценки
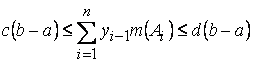 .
.
Следует существование точек верхней граней этих сумм, т.е. интервала Лебега.
Следует заметить, что из существования интеграла Римана следует существование интеграла Лебега, но не наоборот. Так, функции Дирехле, очевидно,
![]()
не интегрируется по Риману, однако ее интервал Либега равен нулю, так как множество рациональных чисел и его мера равна нулю.
Если функция ![]() измерима и интегрируема по Лебегу в степени
измерима и интегрируема по Лебегу в степени ![]()
![]() на
на ![]() , то ее относят к классу
, то ее относят к классу ![]()
![]() .
. ![]()
![]() можно превратить в линейное нормированное пространство, если ввести норму
можно превратить в линейное нормированное пространство, если ввести норму
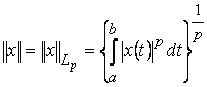 .
.
Множество ![]() , очевидно, замкнуто относительно линейных операций, а нулевым элементом
, очевидно, замкнуто относительно линейных операций, а нулевым элементом ![]() является
является
![]() .
.
В частности, если в примере 1.3 сигналы непрерывны, то в выражении нормы сумма переходит в интеграл
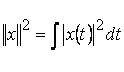 - энергия электрического тока
- энергия электрического тока ![]() , выделенная на единице сопротивления. При
, выделенная на единице сопротивления. При ![]() норма
норма 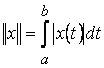 эквивалентна заряду, накопленному на единичной емкости в результате прохождения тока
эквивалентна заряду, накопленному на единичной емкости в результате прохождения тока ![]() .
.
Если ![]() , а
, а ![]() почти всюду ограничена, норму можно ввести как
почти всюду ограничена, норму можно ввести как ![]() , т.е. как наименьшее число
, т.е. как наименьшее число ![]() , для которого неравенство
, для которого неравенство ![]() выполнено почти всюду. В этом случае говорят, что функция
выполнено почти всюду. В этом случае говорят, что функция ![]() принадлежит к классу
принадлежит к классу ![]() . Можно получить, что
. Можно получить, что 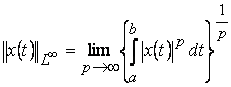 . Таким образом, норма в пространстве
. Таким образом, норма в пространстве ![]() является моделью «амплитуды» функции, в частности, амплитуды колебаний электрического тока, если пренебречь множествами нулевой меры этой функции.
является моделью «амплитуды» функции, в частности, амплитуды колебаний электрического тока, если пренебречь множествами нулевой меры этой функции.
Если функция ![]() интегрируется с весом
интегрируется с весом ![]() , естественно определить норму как
, естественно определить норму как
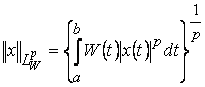 .
.
Это пространство обозначают ![]() .
.
Контрольные вопросы:
1.Что называется элементарным прямоугольником?
2.Мера на элементарных множествах.
3.Свойства измеримых функций.
4.Интеграл Лебега от функции Дирихле.
5.Интегрируема ли эта функция по Риману?