Глава 1. СИГНАЛЫ КАК ЭЛЕМЕНТЫ ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВ

Лекция №1.  

План лекции:

1. Понятия пространства состояний.

2. Метрическое пространство.

3. Нормированное пространство.

4. Примеры пространств состояний.

1.1. Понятие пространства состояний.

Огромное количество технических задач может быть моделировано как трансформация входного сигнала через технический процесс в выходной сигнал с заданными характеристиками. Поскольку технологический процесс может быть организован через сложную структуру, его принято рассматривать как систему, учитывающую те или иные взаимодействия.

Теория систем, как известно [1], предназначена для решения практических задач предсказания поведения процессов и синтеза процессов с требуемым поведением . Реализация основных идей теории систем применительно к динамическим объектам составляет предмет изучения автоматического регулирования в динамических системах.

Рис1.


Математическая модель системы или процесса отражает так или иначе свойства реальной системы, в том числе существующие ограничения. Для построения модели могут быть использованы объекты математического анализа, объединенные в определенные структуры [2].

Поскольку входным сигналом является функция, то для построения модели необходимо воспользоваться структурами  функциональных пространств с введенными там понятиями расстояния (метрическое пространство) и норма (нормированное пространство). Всякая динамическая система проходит через множество состояний . Каждый элемента  характеризует состояние системы в данный момент времени однозначно.

Множество  можно рассматривать как пространство состояний системы.

Поскольку элементами  являются сигналы,  - функциональное пространство в котором целесообразно ввести понятие «близости» элементов, т.е. метрику. Так мы приходим к структуре метрического пространства.

Множество  будет называть метрическим пространством, если каждой паре  элементов из  ставится в соответствие неотрицательное вещественное число , называемое расстоянием (или метрикой) и удовлетворяющее аксиомам:

а) тождества ;

б) симметрии ;

в) треугольника .

Достаточно определить теперь -окрестность точки  как , чтобы легко построить всю теорию сходимости и непрерывности.

Расстояние как функционала в пространстве состояний может быть использовано для решения различных задач оптимизации.

Пространством состояний называется метрическое пространство, каждый элемент которого полностью определяет состояние рассматриваемой системы.

Если ввести в функциональном пространстве линейные операции и понятие, соответствующее «длине» элемента, получим линейное пространство.

Множество  называют линейным нормированным пространством, если в нем отделены линейные операции, удовлетворяющие известным аксиомам линейного векторного пространства и для  -ет неотрицательное число , называемое нормой , которое удовлетворяет следующим условиям:

1) ;

2) ;

3) .

Очевидно всякое нормированное пространство метризума с метриной .

 

ПРИМЕР 1.1.  - совокупность всех функций, непрерывных на  с метриной .

Пространство  нормируемо, норма  удовлетворяет всем аксиомам (1-3).

 

ПРИМЕР 1.2. -мерное евимедово пространство  может быть метридумо с помощью различных метрик:

1.

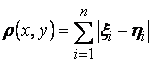
2.

3. 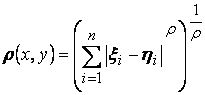,  0 пространство .

Норму естественно ввести с помощью выражения

, .

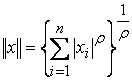Когда количество …………… вектора  счетно, т.е. , а норма определенная как ряд 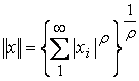, конечна, то соответствующее нормированное пространство обозначают .

 

ПРИМЕР 1.3. В качестве примера пространства состоят рассмотренное функциональное пространство импульсных сигналов продолжительностью  , появляющиеся через один и тот же промежуток времени , амплитуда -го сигнала :

Так как сигналы квантованы во времени, относительной моделью является пространство  (см. пр. 1.2), если в качестве нормы рассмотреть 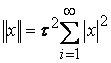 (*). Если  - электрический ток, протекающий через единичное сопротивление, то энергия, выделяющаяся на этом сопротивлении, соответствует .

Если сигналы непрерывны, , , сумма (*) переходит в интервал Лебега, более общий, чем интервал Римана.

 

Контрольные вопросы:

1.     Определение пространства состояний системы.

2.     Что составляет предмет изучения автоматического регулирования в динамических системах.

3.     Приведите примеры пространств состояний для сигналов, квантованных во времени.