Главная страница О курсе Введение Программа по курсу математики для студентов второго курса заочного факультета Литература Задания для контрольных работ Методические указания к выполнению контрольных работ			Дискретная математика Задание 1. Составить таблицы истинности для формул. Составим таблицу истинности для формулы 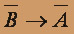: 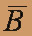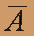B A 0 0 1 1 1 0 1 1 0 0 1 0 0 1 1 1 1 0 0 1 Задание 2. Упростить формулы. Для упрощения формулы попробуем исключить импликацию: 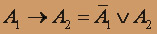и используем основные логические эквивалентности.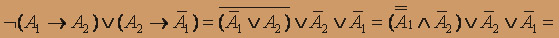 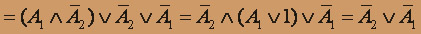Задание 3.Проверить линейность, монотонность и самодвойственность логических функций. Проверим линейность логической функции f(x1,x2 )= . Для этого приведем соответствующую формулу к дизъюнктивной нормальной форме = = 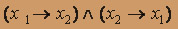. 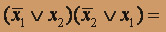Далее используем соотношения алгебры Жегалкина 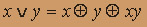,,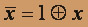 x + x = 0 . Получаем 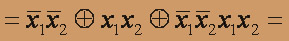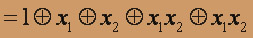=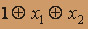. Следовательно, рассматриваемая функция является линейной. Для определения монотонности f(x1,x2) составим ее таблицу истинности. x1 x2 0 0 1 0 1 0 1 0 0 1 1 1 Поскольку (0,0) < (0,1), f(0,0) > f(0,1), то функция не монотонна. Выясним, является ли f самодвойственной. Для этого построим таблицу истинности для 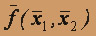и проверим равенство f(x1, x2) = 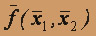. 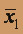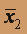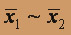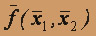1 1 1 0 1 0 0 1 0 1 0 1 0 0 1 0 Так как 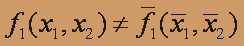, то f несамодвойственна. Задание 4.Упростить схемы. 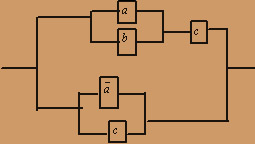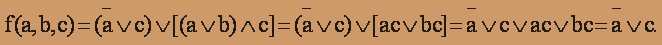Составим функцию проводимости для схемы, учитывая, что параллельное соединение переключателей описывается дизъюнкцией (V), а последовательное конъюнкцией (^): Полученной формуле соответствует схема: Задание 5.Составить матрицу инцидентности и смежности для графов. 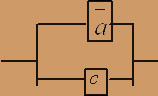В приведенных графах вершины пронумерованы арабскими цифрами и расположены на пересечении ребер. Для построения матриц инцидентности и смежности сначала упорядочим все ребра ek , определяемые парами вершин (i,j), произвольным образом. 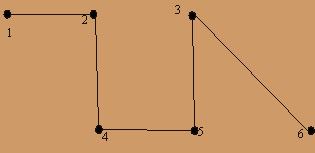Например, для графа G: e1 = (1,2), e2 =(2,4), e3 =(4,5), e4 =(3,5). e5 =(3,6). Строки матрицы инцидентности помечаются вершинами графа, а столбцы ребрами. Матрица имеет размер m x n, где m - количество вершин графа, n- число ребер. Считается, что вершины и ребра пронумерованы. Элемент i – ой строки и j- го столбца равен 1, если i – ая вершина инцидентна j- му ребру, и равен 0 в противном случае. Матрица А графа G имеет вид: e1 e2 e3 e4 e5 A= В матрице смежности В строки и столбцы помечаются номерами вершин в порядке их возрастания. Элемент bij равен количеству ребер, соединяющих вершину с номером i с вершиной j. 1 2 3 4 5 Задание 6.По матрице инцидентности А и матрице смежности B построить неориентированные графы. В матрице инцидентности столбцам соответствуют вершины графа, строкам – ребра. По матрице инцидентности А= построить граф. В матрице 4 столбца и 3 строки, следовательно, в графе 4 вершины и 3 ребра: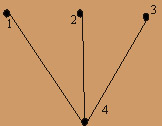 Строке 1 матрицы соответствует ребро (1,4), строке 2 – ребро (2,4), строке 3 – ребро (4,3). 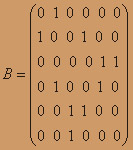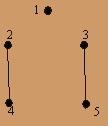По матрице смежности В= построить граф. В матрице смежности строкам и столбцам соответствуют вершины графа. Если bij = с, то вершине i и вершине j инцидентны с – ребер. Поскольку размер В 5x5, то граф имеет 5 вершин. Из первой строки следует, что вершина 1 изолированная, из второй строки видно, что вершина 2 и вершина 4 соединены ребром, из третьей строки видно, что вершина 3 и вершина 5 тоже соединены ребром.