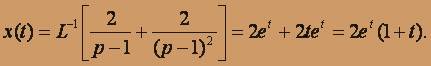О курсе
Введение
Программа по курсу математики для студентов второго курса заочного факультета
Литература
Задания для контрольных работ
Методические указания к выполнению контрольных работ
а) f(t) = sh t cos 5t.
Известно, что sh = (et - e- t)/ 2, тогда f(t) = 1 / 2 [etcos 5t - e- tcos 5t].
По таблице изображений
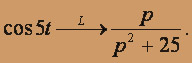По теореме смещения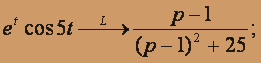 
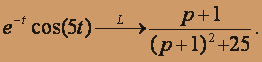
Отсюда получаем искомое изображение в виде
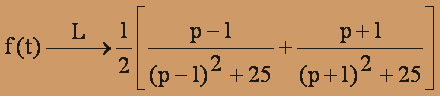
б) f(t) = tch t sin 2t.
Выражаем
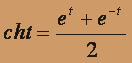, тогда f(t) = (t / 2)[etsin 2t + e- t sin 2t].По таблице изображения
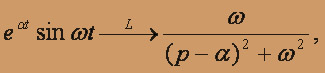тогда 
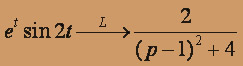
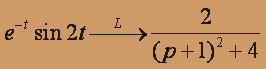
Имеем:
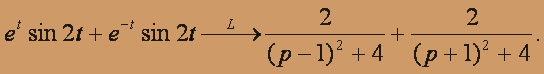
По теореме о дифференцировании изображений определяем искомое изображение
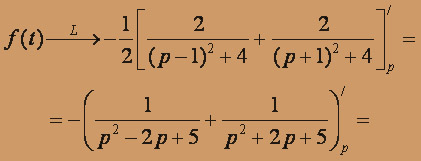
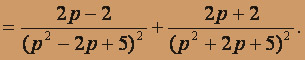
в) f(t) = sh 3t / t По таблице определяем
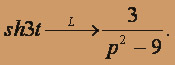По теореме об интегрировании изображений определяем искомое изображение: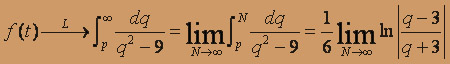
= 
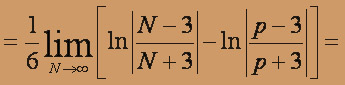
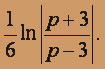
а)
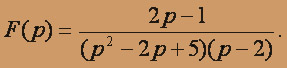
Применяя метод неопределенных коэффициентов, разложим данную правильную дробно-рациональную функцию на простые дроби:
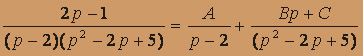
2p - 1 = A(p2 - 2p + 5) + (Bp + c)(p - 2)
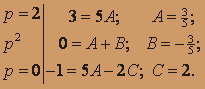
Получаем:
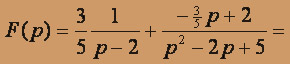
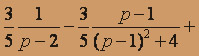
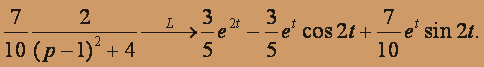
б) F(p)= 1 / (p2+ 1)3.Корни знаменателя p=
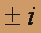кратности 3. Применяем формулу обращения для случая кратных корней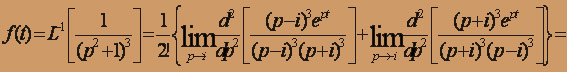
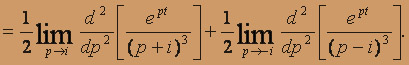
После двукратного дифференцирования и перехода к пределу находим
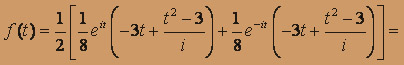
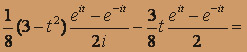1 / 8 (3 - t2)sin t - 3/8 t cos t.
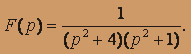
Так как
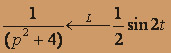и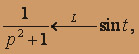 
то применяя свертку, определяем искомый оригинал.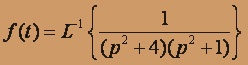
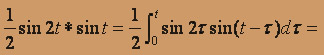
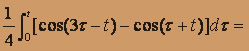
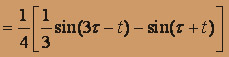
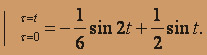
x'' + 3x' + 2x = tet; x(0) = 0; x'(0) = 1. Пологая
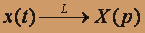по правилу дифференцирования оригинала имеем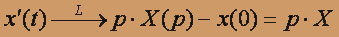 
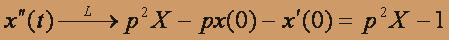
Перейдем к изображению в правой части уравнения.
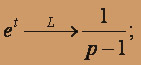
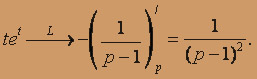
Теперь заданное уравнение можно представить в операторной форме:
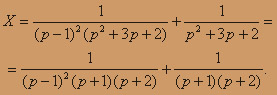
Определяем оригинал:
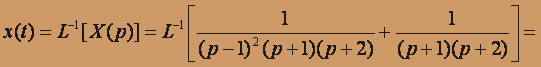
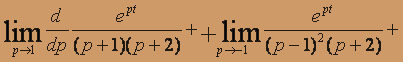
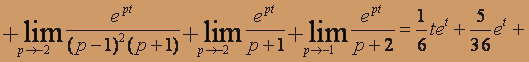
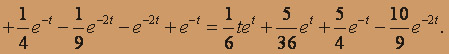
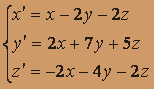
при начальных условиях x(0) = 0; y(0) = 3, z(0) = -2 Перейдем в системе к изображениям. Пусть
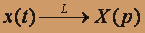
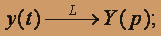
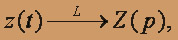тогда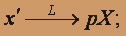 
; y' = pY - 3; z' = pZ + 2. Приходим к следующей операторной системе: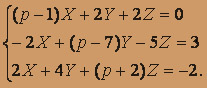
Решая ее, получим:
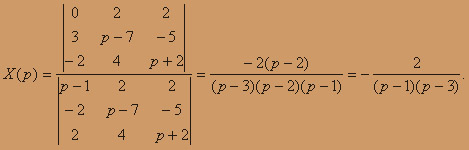
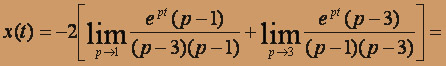
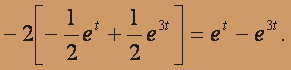
Аналогично нетрудно найти следующие выражения для остальных переменных:
z(t) = - 2et - 2e2t - 2e3t
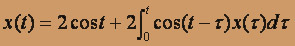
Для данного уравнения
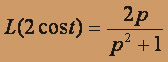
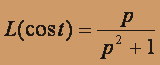
Поэтому, переходя к изображениям в исходном уравнении, получим:
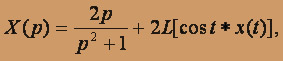
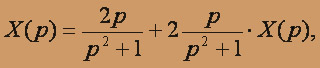
тогда
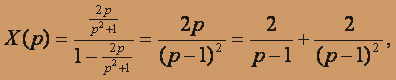
переходя к оригиналу, получим:
