Главная страница О курсе Введение Программа по курсу математики для студентов второго курса заочного факультета Литература Задания для контрольных работ Методические указания к выполнению контрольных работ			Теория функций комплексного переменного Задание 1. Даны: z1= 1 + i, z2= 3i - 1, z3 = 2 - 3i, z4 = 5 - 3i, z5 = i - 6, z6 = 2i, z7 = 3, z8 = - i. Вычислить: 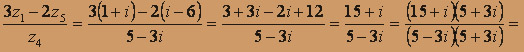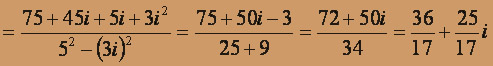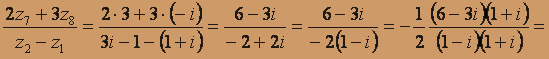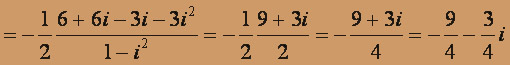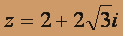Задание 2. Возвести комплексное число z в степень. , z5 - ? z = x + iy = 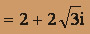- алгебраическая форма комплексного числа.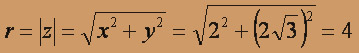 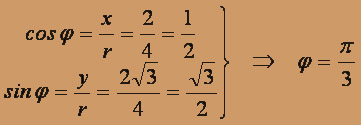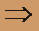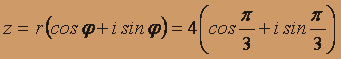- тригонометрическая форма комплексного числа. Далее, по формуле возведения комплексного числа в n-ую степень, имеем: Задание 3.Найти корни уравнения z6 - iz3 + 6 = 0. 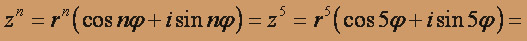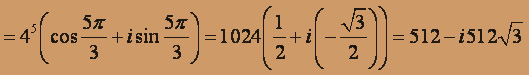Пусть t = z3, тогда t2 - it + 6 = 0, откуда t1 = 3i; t2 = -2i, следовательно z13 = 3i, z23 = - 2i. 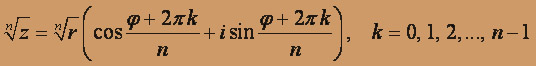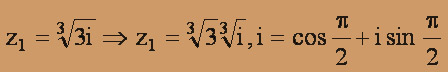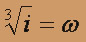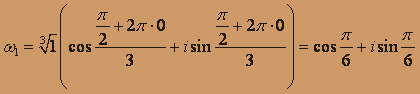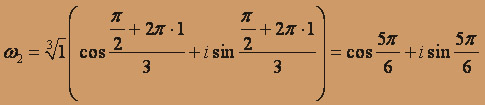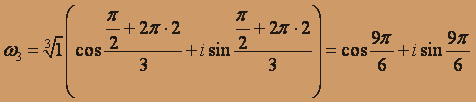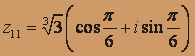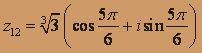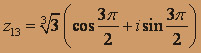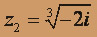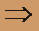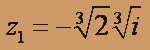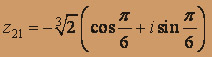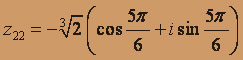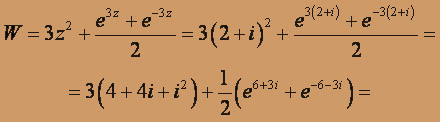Тогда, по формуле будем иметь: Пусть , тогда имеем три значения корня: Таким образом, Аналогично, , следовательно Задание 4. Вычислить значение функции W = f(z) в точке z0. W = 3z2 + ch3z; z0 = 2 + i (т.к. 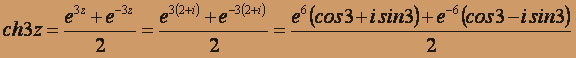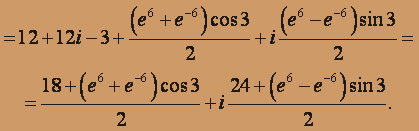) Задание 5.Проверить выполнение условий Коши-Римана и там, где они выполняются, найти производную: f (z) = ez Пусть f(z) = u(x,y) + iv(x,y). Так как ez = ex + iy = sxcos y + iex sin y, то u(x,y) = ex cos y, v(x,y) = ex sin y. 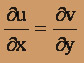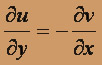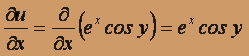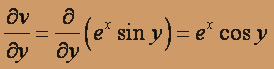Найдём частные производные и выясним, в окрестности каких точек они существуют и непрерывны, а также в каких точках плоскости выполняются условия Коши-Римана , : , т.е. 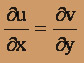для любых действительных x и y, и эти частные производные непрерывны во всей плоскости R2; кроме того, 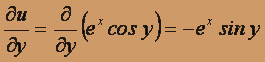, , 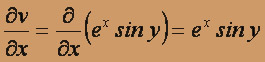т.е. 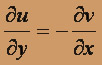для любых действительных x и y, и эти частные производные непрерывны во всей плоскости R2. 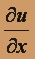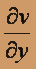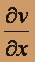Так как условия Коши-Римана выполняются для любой пары действительных чисел (x,y) и частные производные , , , существуют и непрерывны в окрестности любой точки (x,y), то производная f '(z) существует в любой точке z = x + iy комплексной плоскости C. 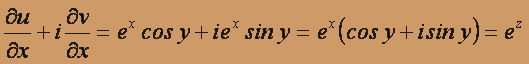Найдём эту производную: f '(z) = Итак, f '(z) = (ez)' = ez, . Задание 6.Вычислить интеграл вдоль кривой l от точки z0 до точки z1: где l: Im z = Re z + 1; z0 = 1 + 2i, z1 = 2 = 3i. z = x + iy x = Re z, y = Im z l: y = x + 1 от точки (1;2) до точки (2;3). Задание 7.Найти разложение функции в ряд Лорана в окрестности z0. Указать главную и правильную части ряда и его область сходимости. Выписать значение вычета. f(z) = 2 / z(3 - z), z0= 0. 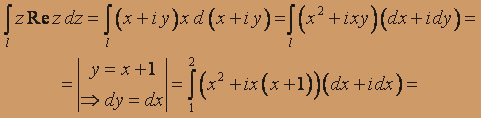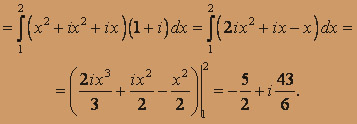Предварительно представим данную дробь в виде суммы двух простейших дробей 2 / z(3 - z) = A / z + B / (3 - z). Найдём числа A и B: 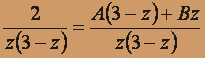следовательно, 0 z + 2 = (B - A)z + 3A , откуда 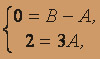т.е. A = B = 2 / 3. 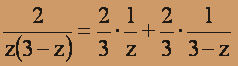Итак, Так как дробь (2/3)/z уже представлена в виде суммы (состоящей из одного слагаемого) членов вида cnzn , то остаётся найти разложение дроби (2/3)/(3 - z) . Для этого воспользуемся разложением дроби 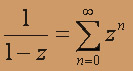в бесконечно убывающую геометрическую прогрессию со знаменателем q = z в той области, где z – “мало” (т.е. в открытом круге q = |z| < 1 ) и получим: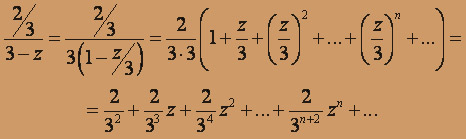 Этот ряд сходится при | q |<| z / 3 | < 1, т.е. в открытом круге | z | < 3. 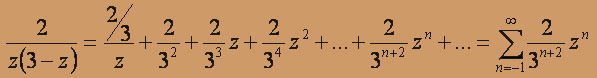Теперь запишем ряд Лорана для исходной дроби: Область сходимости этого ряда – кольцо 0 < |z| < 3 . Первое слагаемое, (2/3)/z , является главной частью ряда, оставшаяся часть ряда – правильной 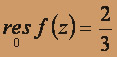. 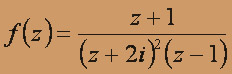Задание 8.Определить тип всех особых точек и вычислить вычет функции, найти вычет в бесконечно удалённой точке. Особыми точками функции f(z) , очевидно, являются следующие точки: - 2i полюс 2-ого порядка, l - полюс 1-ого порядка. 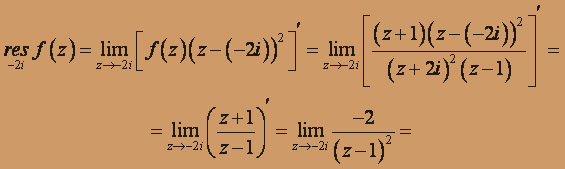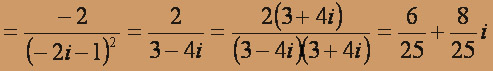Найдём вычет в точке - 2i: Найдём вычет в точке 1, записав функцию f(z) в ви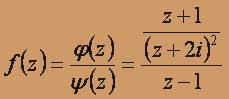де , где 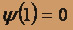, , 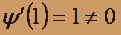тогда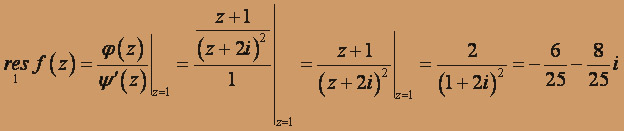 Найдём вычет в бесконечно удалённой точке: