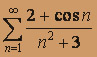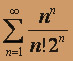Главная страница О курсе Введение Программа по курсу математики для студентов второго курса заочного факультета Литература Задания для контрольных работ Методические указания к выполнению контрольных работ			Ряды Задание 1. Исследовать сходимость рядов: а)б) в)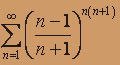 а) Поскольку an > 0, то для исследования сходимости ряда 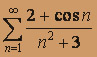можно применить первый признак сравнения. В качестве "эталонного" ряда берем 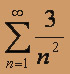- обобщенный гармонический ряд, он сходится (показатель степени гармонического ряда p = 2 > 1), следовательно, по первому признаку сравнения сходится и "меньший", исходный ряд 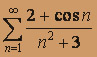. б) Ряд 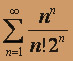- с положительными членами. Для исследования его сходимости удобно применять признак Даламбера. Записываем n-ый член ряда: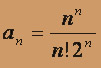. Вычисляем an + 1 : 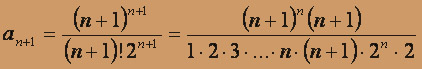. 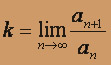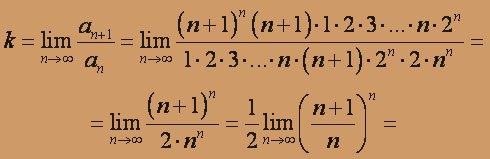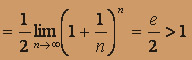Найдем : 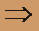, исходный ряд 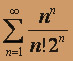расходится. в) Ряд 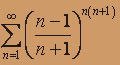- с положительными членами. Для исследования его сходимости удобно применять радикальный признак Коши. 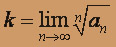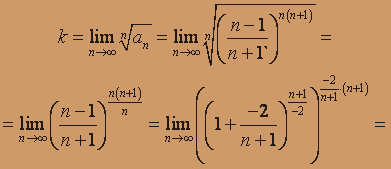Вычисляем : 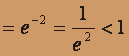, 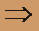исходный ряд 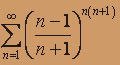сходится. 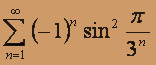Задание 2. Исследовать сходимость знакочередующихся рядов, выяснить характер сходимости: а)б) 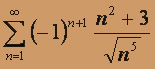а) 1. Проверим выполнение необходимого условия сходимости: найдем предел общего члена ряда. 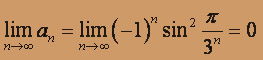. Необходимое условие выполнено. 2. Исследование сходимости знакочередующегося ряда можно начинать с проверки абсолютной сходимости. Если ряд, составленный из абсолютных величин, сходится, то и сам ряд сходится. Если же окажется, что данный знакочередующийся ряд не обладает абсолютной сходимостью, то исследование продолжают с помощью признака Лейбница. Исследуем сходимость ряда, составленного из модулей: 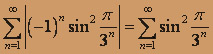, 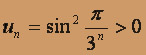. при всех 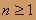. 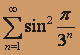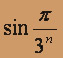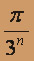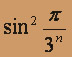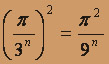Для исследования на сходимость ряда можно применить второй признак сравнения: при , при ; используемый для сравнения "эталонный" ряд 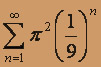, с общим членом 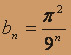, является геометрической прогрессией со знаменателем q = 1 / 9 < 1 , которая есть ряд сходящийся. Вычислим 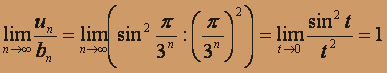(применили 1-й замечательный предел). Следовательно, по второму признаку сравнения ряд 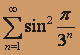, составленный из модулей, так же сходящийся. А значит, исходный знакочередующийся ряд 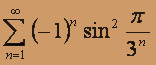сходится абсолютно. б) 1. Проверим выполнение необходимого условия сходимости: найдем предел общего члена ряда. 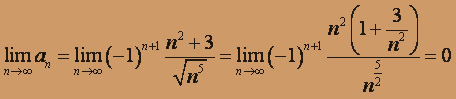Необходимое условие выполнено. 2. Исследуем сходимость ряда, составленного из модулей: 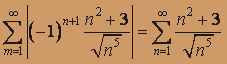, 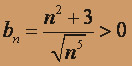при всех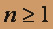 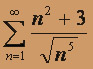Для исследования сходимости ряда можно применить первый признак сравнения: имеем 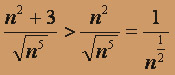, т.е. каждый член ряда из абсолютных значений исходного ряда 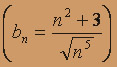больше соответствующего члена обобщенного гармонического ряда 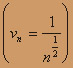. Так как "меньший" "эталонный" гармонический ряд 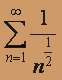расходится (показатель степени гармонического ряда p = 1 / 2 < 1 ), то по первому признаку сравнения "больший" ряд 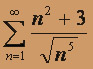также расходится. Следовательно, исходный знакочередующийся ряд 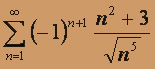абсолютно не сходится. 3. Продолжим исследование с помощью признака Лейбница знако-чередующегося ряда 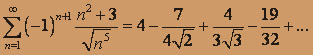. а) 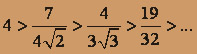, т.е. члены исходного знакочередующегося ряда убывают по абсолютному значению. б) 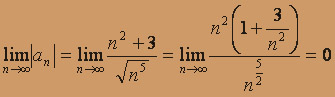. Итак, для данного знакочередующегося ряда 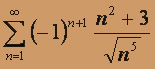выполнены оба условия, содержащиеся в признаке Лейбница, значит, этот ряд сходится. Из этого и из того, что ряд не является абсолютно сходящимся, окончательно следует, что ряд сходится условно. 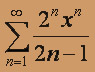Задание 3.Определить интервал сходимости ряда и исследовать сходимость на концах интервала: а)б) 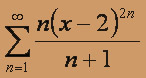а) 1. Если степенной ряд при фиксированном x сходится, то он сходится, и притом абсолютно (из теоремы Абеля) в интервале (- X, X) . Поэтому исследуем ряд 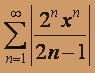, составленный из абсолютных величин членов исходного ряда. К нему можно применить признак Даламбера, для чего находим 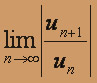. 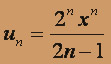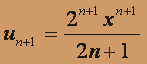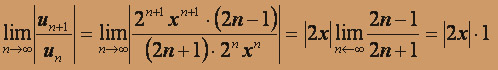По признаку Даламбера ряд будет сходиться, если |2x| < 1 , - 1 < 2x < 1 , - 1 / 2 < x < 1 / 2 - интервал сходимости. 2. Исследуем сходимость ряда в граничных точках интервала сходимости. 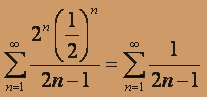В точке x = 1 / 2 получим числовой знакоположительный ряд: Сравним его с расходящимся гармоническим рядом 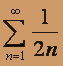, bn = 1 / 2n , поскольку an = 1 / (2n - 1) > 1 / 2n = bn , то по первому признаку сравнения ряд 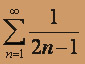расходится. 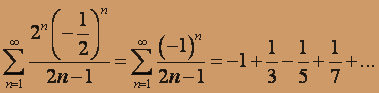В точке x = - 1 / 2 получим знакочередующийся ряд Этот ряд по признаку Лейбница сходится, т.к. выполнены оба условия: 1) 1 > 1 / 3 > 1 / 5 > 1 / 7 > ...; 2) 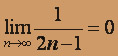. Окончательно получаем область сходимости исходного ряда, промежуток [ - 1 / 2 ; 1 / 2 ). б) 1. Исследуем на сходимость ряд 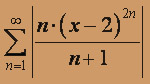, составленный из абсолютных величин членов исходного ряда. К нему удобно применить радикальный признак Коши, для чего вычислим 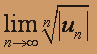: 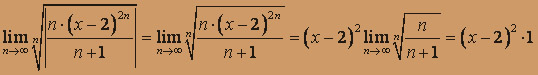. Ряд будет сходиться, если (x - 2)2 < 1 , |x - 2| < 1, - 1 < x - 2 < 1, 1 < x < 3. Итак, при 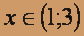ряд сходится абсолютно. 2. Исследуем сходимость ряда в граничных точках интервала сходимости. В точке x = 3 получим числовой знакоположительный ряд 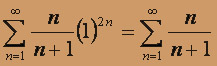. В точке x = 1 получим числовой знакоположительный ряд 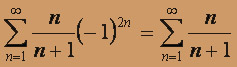. Эти ряды расходятся, т.к. не выполнено необходимое условие сходимости рядов: 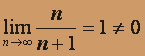. Окончательно получаем область сходимости исходного ряда - интервал (1;3). Задание 4. Пользуясь разложением в ряд Маклорена функций ex, sin x, cos x, ln(1 + x), (1 + x)m, arctg x, разложить данные функции в ряд: а) f(x) = x cos 2x; б) f(x) = ln ((1 + x) / (1 - x)). 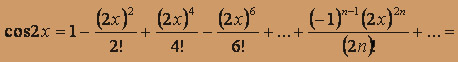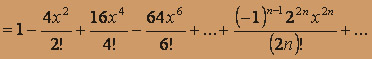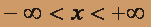а) В ряде Маклорена для cos x заменяем x на 2x, тогда , Умножим обе части равенства на x : 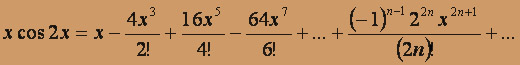, 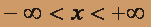или 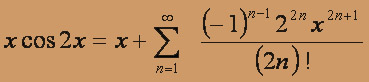, 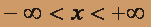. б) Преобразуем данную функцию: ln ((1 + x) / (1 - x) ) = ln (1 + x) - ln (1 - x). 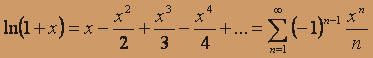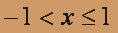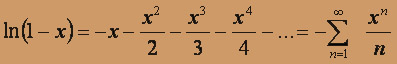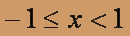Запишем ряды Маклорена для полученных функций: Вычитая эти ряды почленно, имеем 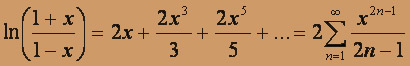, - 1 < x < 1. 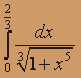Задание 5. Пользуясь формулами разложения функций в ряд Маклорена, вычислить интеграл с точностью до 0,001. 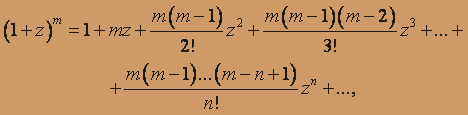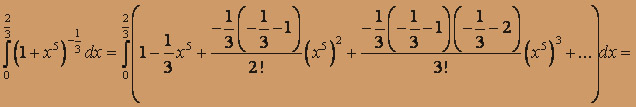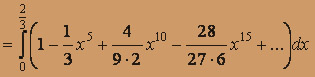Разложим подынтегральную функцию в биномиальный ряд - 1 < z < 1, полагая в нем z = x5, m = - 1 / 3 имеем (1 + x5)- 1 / 3 и Степенной ряд можно интегрировать почленно по любому отрезку, при-надлежащему интервалу сходимости. Выполняя почленно интегрирование, имеем: 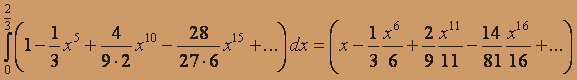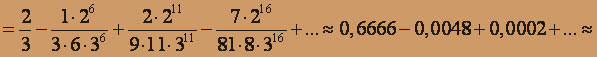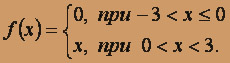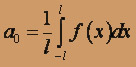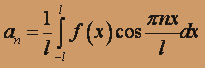Так как третий член по абсолютной величине меньше заданной погрешности (0.0002 < 0.001), то оставили первые два члена, остальные члены отбросили, ибо ряд знакочередующийся, следовательно, его остаточный член не превысит первого отброшенного члена (следствие из теоремы Лейбница). Вычисляя три последовательных первых членов полученного знакочередующегося сходящегося ряда, сохраняем четыре цифры после запятой, при этом округляя, в ответе имеем три верных десятичных знака. Задание 6.Разложить данную функцию в ряд Фурье в указанном интервале Данная функция удовлетворяет условиям теоремы Дирихле, следовательно, для нее существует ряд Фурье. Найдем его. 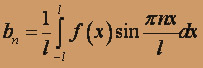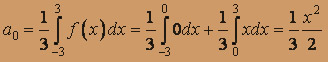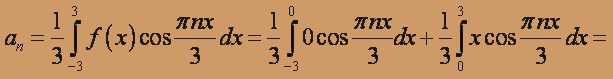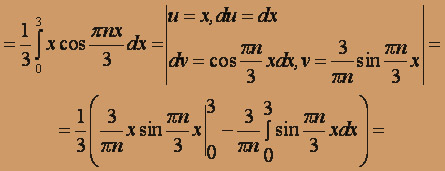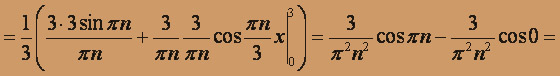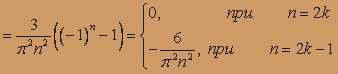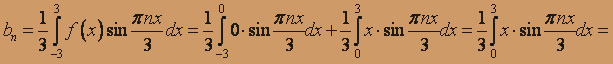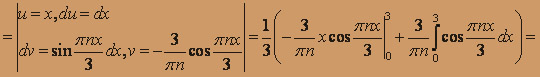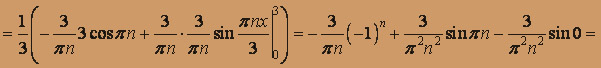Данная функция не является ни четной, ни нечетной, поэтому коэффициенты Фурье находим по формулам: , Итак, , (k = 1,2,...) 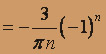, n = 1, 2, ..., Ряд Фурье для функции 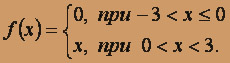имеет вид: